Analysis - 15 BE
Aufgabe 1
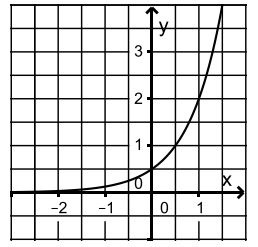
Die gegebene Funktion ist \( f(x) = a \cdot b^x \). Die Werte von \( a \) und \( b \) sollen bestimmt werden.
1. Ermitteln der Werte anhand des gegebenen Graphen:
- Bei \( x = 0 \), \( f(0) = a \). Der Graph zeigt, dass \( f(0) = 1 \).
- Bei \( x = 1 \), \( f(1) = a \cdot b \). Der Graph zeigt, dass \( f(1) = 2 \).
2. Einsetzen der bekannten Werte:
Bei \( x = 0 \): \( f(0) = a = 1 \)
Also \( a = 1 \).
Bei \( x = 1 \): \( f(1) = 1 \cdot b = 2 \)
Also \( b = 2 \).
Antwort a):
Die Werte für \( a \) und \( b \) sind:
\[ a = 1 \]
\[ b = 2 \]
b) Der Graph der in \( \mathbb{R} \) definierten Funktion \( g \) mit \( g(x) = 3^x \) wird um 2 in negative x-Richtung verschoben. Zeigen Sie, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von \( g \) in y-Richtung erzeugt werden kann.
Die Funktion \( g(x) = 3^x \) wird um 2 in negative x-Richtung verschoben. Die resultierende Funktion ist \( g(x+2) \).
1. Zeichne den Graphen von \( g(x+2) \). Dies würde den Graphen von \( g(x) \) um 2 Einheiten nach links verschieben.
2. Zeigen, dass der neue Graph auch durch eine Streckung des Graphen von \( g \) in y-Richtung erzeugt werden kann:
- Die Streckung in y-Richtung wird durch Multiplizieren der Funktion mit einem Faktor dargestellt.
- Die neue Funktion ist: \( y = c \cdot 3^{x+2} \).
- Vergleichen Sie die Werte von \( g(x+2) \) und \( c \cdot 3^{x+2} \), um \( c \) zu bestimmen.
Einsetzen von \( x = 0 \) in beide Funktionen:
\( g(0+2) = 3^2 = 9 \)
\( c \cdot 3^{0+2} = c \cdot 9 \)
Da die Graphen identisch sind, muss \( c \cdot 9 = 9 \) sein.
Also ist \( c = 1 \).
Antwort b):
Der Graph von \( g(x) = 3^x \), um 2 Einheiten in negative x-Richtung verschoben, ist identisch mit dem Graphen von \( g(x) \) selbst, da eine Verschiebung in x-Richtung keine Änderung in y-Richtung verursacht. Das bedeutet, dass keine Streckung in y-Richtung nötig ist, um den neuen Graphen zu erzeugen.
Aufgabe 2:
a) Eine ganzrationale Funktion \( f \) hat die Nullstellen 1, 2 und –3. Geben Sie eine Funktionsgleichung für \( f \) an.
Eine ganzrationale Funktion \( f \) hat die Nullstellen 1, 2 und –3.
1. Die Nullstellenform einer Funktion lautet:
\[ f(x) = a \cdot (x - x_1) \cdot (x - x_2) \cdot (x - x_3) \]
wobei \( x_1, x_2, x_3 \) die Nullstellen sind.
2. Einsetzen der gegebenen Nullstellen:
\[ f(x) = a \cdot (x - 1) \cdot (x - 2) \cdot (x + 3) \]
Da keine weiteren Informationen über den Streckfaktor \( a \) gegeben sind, kann \( a \) als beliebige Konstante betrachtet werden.
Antwort a):
Eine mögliche Funktionsgleichung für \( f \) ist:
\[ f(x) = a \cdot (x - 1) \cdot (x - 2) \cdot (x + 3) \]
b) Für eine Funktion \( h \) gilt: \( h'(x) = x^2 - 2x - 24 \). Bestimmen Sie die Extremstellen des Graphen von \( h \).
Für eine Funktion \( h \) gilt: \( h'(x) = x^2 - 2x - 24 \)
Bestimmen Sie die Extremstellen des Graphen von \( h \).
1. Die Extremstellen (Hoch- oder Tiefpunkte) treten auf, wenn die erste Ableitung \( h'(x) \) den Wert 0 hat. Daher setzen wir \( h'(x) = 0 \).
\[ x^2 - 2x - 24 = 0 \]
2. Lösung der quadratischen Gleichung mithilfe der Mitternachtsformel (quadratische Lösungsformel):
\[ x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
wobei \( a = 1, b = -2 \) und \( c = -24 \) sind.
Einsetzen ergibt:
\[ x_{1,2} = \frac{2 \pm \sqrt{4 + 96}}{2} \]
\[ x_{1,2} = \frac{2 \pm 10}{2} \]
Daraus folgt:
\[ x_1 = 6 \]
\[ x_2 = -4 \]
Antwort b):
Die Extremstellen des Graphen von \( h \) sind bei \( x = 6 \) und \( x = -4 \). Ob es sich um Hoch- oder Tiefpunkte handelt, müsste durch die Untersuchung der zweiten Ableitung oder durch den Vorzeichenwechsel der ersten Ableitung ermittelt werden.
Aufgabe 3
Gegeben ist die in \( \mathbb{R} \) definierte Funktion \( f \) mit \( f(x) = x^2 \). Bestimmen Sie diejenige reelle Zahl \( m \) mit \( m < 0 \), für die der Graph von \( f \) und die Gerade mit der Gleichung \( y = m \cdot x \) eine Fläche mit dem Inhalt 36 einschließen.
1. Setzen Sie \( f(x) \) und \( y = m \cdot x \) gleich:
\[ x^2 = m \cdot x \]
Dies führt zu:
\[ x^2 - m \cdot x = 0 \]
Dies kann als \( x(x - m) = 0 \) geschrieben werden.
Da \( x = 0 \) bereits bekannt ist (Ursprung), ist der andere Schnittpunkt \( x_1 = m \).
2. Berechnen Sie die Fläche zwischen den beiden Kurven vom Punkt \( m \) bis zum Ursprung:
\[ A = \int_{m}^{0} (m \cdot x - x^2) \, dx \]
Integrieren:
\[ A = \left[ \frac{m \cdot x^2}{2} - \frac{x^3}{3} \right]_{m}^{0} \]
3. Setzen Sie die Integrationsgrenzen ein und vereinfachen:
\[ A = \left( \frac{m \cdot 0^2}{2} - \frac{0^3}{3} \right) - \left( \frac{m \cdot m^2}{2} - \frac{m^3}{3} \right) \]
\[ A = -\left( \frac{m^3}{2} - \frac{m^3}{3} \right) \]
\[ A = -\left( \frac{m^3}{6} \right) \]
4. Setzen Sie \( A = 36 \) und lösen Sie die Gleichung:
\[ -\frac{m^3}{6} = 36 \]
\[ m^3 = -216 \]
\[ m = -6 \]
Antwort:
Die reelle Zahl \( m \) mit \( m < 0 \), für die der Graph von \( f \) und die Gerade \( y = m \cdot x \) eine Fläche von 36 einschließen, ist \( m = -6 \).
Stochastik - 10 BE
Aufgabe 1
In einer Gemeinde gab es beim Streit um ein neues Bauprojekt eine Befragung. Von den Teilnehmenden waren 70 % älter als 35 Jahre. 60 % der höchstens 35-Jährigen und 20 % der über 35-Jährigen, die an der Befragung teilnahmen, stimmten gegen das Bauprojekt.
a) Bestimmen Sie das Ergebnis der Befragung.
b) Bestimmen Sie unter den Teilnehmenden, die für das Projekt stimmten, den Anteil der höchstens 35-Jährigen.
Nehmen wir an, es haben insgesamt 100 Personen an der Umfrage teilgenommen (dies vereinfacht die Berechnung und ändert nichts am prozentualen Ergebnis).
a) Bestimmen Sie das Ergebnis der Befragung:
- Anzahl der Personen älter als 35 Jahre: \(0,70 \times 100 = 70\)
- Anzahl der Personen höchstens 35 Jahre alt: \(100 - 70 = 30\)
- Anzahl der höchstens 35-Jährigen, die gegen das Projekt stimmten: \(0,60 \times 30 = 18\)
- Anzahl der über 35-Jährigen, die gegen das Projekt stimmten: \(0,20 \times 70 = 14\)
Gesamtzahl der Personen, die gegen das Projekt stimmten: \(18 + 14 = 32\)
Prozentsatz gegen das Projekt: \(32\% \)
Prozentsatz für das Projekt: \(100\% - 32\% = 68\% \)
b) Bestimmen Sie unter den Teilnehmenden, die für das Projekt stimmten, den Anteil der höchstens 35-Jährigen:
Anzahl der höchstens 35-Jährigen, die für das Projekt stimmten: \(30 - 18 = 12\)
Anteil der höchstens 35-Jährigen, die für das Projekt stimmten, im Verhältnis zu allen, die dafür stimmten:
\[\frac{12}{68} = 0,1765 \approx 17,65\%\]
Antworten:
a) 32% der Befragten stimmten gegen das Projekt, während 68% dafür stimmten.
b) Unter den Teilnehmenden, die für das Projekt stimmten, waren ca. 17,65% höchstens 35 Jahre alt.
Aufgabe 2
Für ein Zufallsexperiment wird eine Zufallsgröße \( X \) festgelegt, welche die drei Werte 2, 5 und 8 annehmen kann. In der Abbildung ist die Wahrscheinlichkeitsverteilung von \( X \) dargestellt.
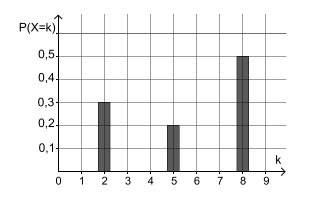
a) Geben Sie die in der Tabelle fehlenden Werte an. Berechnen Sie den Erwartungswert von \( X \).
b) Das Zufallsexperiment wird zweimal unter gleichen Bedingungen durchgeführt. Dabei wird jeweils der Wert der Zufallsgröße \( X \) notiert. Bestimmen Sie die Wahrscheinlichkeit dafür, dass das Produkt dieser beiden Werte den Wert 10 ergibt.
a) Geben Sie die in der Tabelle fehlenden Werte an
Die Gesamtwahrscheinlichkeit aller möglichen Werte von \( X \) muss 1 ergeben. Die Wahrscheinlichkeit für \( X = 5 \) ist bereits als 0,2 gegeben. Aus der Grafik können wir entnehmen, dass die Wahrscheinlichkeit für \( X = 8 \) 0,5 beträgt und die Wahrscheinlichkeit für \( X= 2\) etwa 0,3 ist.
Erwartungswert von \( X \):
\[ E(X) = \sum_{k} k \times P(X = k) \]
\[ E(X) = 2 \times 0,3 + 5 \times 0,2 + 8 \times 0,5 \]
\[ E(X) = 0,6 + 1 + 4 = 5,6 \]
a)
\( E(X) = 5,6 \)
b) Wahrscheinlichkeit für das Produkt von zwei Werten, die 10 ergeben:
Um das Produkt von 10 zu erhalten, können die beiden Werte nur \( (2,5) \) oder \( (5,2) \) sein.
Die Wahrscheinlichkeit, dass \( X \) in einem Versuch den Wert 2 und in einem anderen Versuch den Wert 5 annimmt, beträgt:
\[ P(X_1 = 2 \text{ und } X_2 = 5) = P(X = 2) \times P(X = 5) = 0,3 \times 0,2 = 0,06 \]
Die Wahrscheinlichkeit für \( (5,2) \) ist gleich der für \( (2,5) \), da sie unabhängige Ereignisse sind:
\[ P(X_1 = 5 \text{ und } X_2 = 2) = 0,06 \]
Die gesuchte Gesamtwahrscheinlichkeit beträgt:
\[ P = 0,06 + 0,06 = 0,12 \]
b)
Die Wahrscheinlichkeit, dass das Produkt der beiden Werte 10 ergibt, beträgt \( 0,12 \).
Lineare Algebra - 10 BE
Aufgabe 1
Gegeben sind die Punkte \( A(0 | 0) \), \( B(8 | 6) \) und \( C(4 | 3 | z) \), wobei \( z \) eine positive reelle Zahl ist.
a) Zeigen Sie, dass es sich bei dem Dreieck \( ABC \) um ein gleichschenkliges Dreieck mit der Basis \( AB \) handelt.
Zeigen, dass \( ABC \) ein gleichschenkliges Dreieck mit Basis \( AB \) ist.
Länge der Strecken berechnen:
Die Länge einer Strecke zwischen zwei Punkten \( (x_1, y_1) \) und \( (x_2, y_2) \) ist durch den Satz des Pythagoras gegeben:
\[d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]
1. Strecke \( AB \):
\[AB = \sqrt{(8 - 0)^2 + (6 - 0)^2} = \sqrt{64 + 36} = \sqrt{100} = 10\]
2. Strecke \( AC \):
\[AC = \sqrt{(4 - 0)^2 + (3 - 0)^2 + z^2} = \sqrt{16 + 9 + z^2} = \sqrt{25 + z^2}\]
3. Strecke \( BC \):
\[BC = \sqrt{(8 - 4)^2 + (6 - 3)^2 + z^2} = \sqrt{16 + 9 + z^2} = \sqrt{25 + z^2}\]
Da \( AC \) und \( BC \) die gleiche Länge haben, ist das Dreieck \( ABC \) gleichschenklig mit der Basis \( AB \).
b) Das Dreieck \( ABC \) hat den Flächeninhalt 35. Bestimmen Sie den Wert von \( z \).
b)
Ziel: Bestimme \( z \) so, dass der Flächeninhalt von \( ABC \) gleich 35 ist.
Flächeninhalt von \( ABC \) berechnen:
Für ein Dreieck mit der Basis \( b \) und der Höhe \( h \) gilt:
\[A = \frac{1}{2} b \times h\]
Die Höhe \( h \) des Dreiecks vom Punkt \( C \) zur Basis \( AB \) ist gleich dem z-Wert von Punkt \( C \).
Da die Fläche 35 beträgt und die Basis \( AB \) eine Länge von 10 hat:
\[35 = \frac{1}{2} \times 10 \times h \implies h = 7\]
Somit ist \( z = 7 \).
Antwort b)
Der Wert von \( z \) beträgt 7.
Aufgabe 2
Gegeben sind die Punkte \( P(2 | 0 | 1) \) und \( Q(2 | 4 | 9) \) sowie die parallelen Geraden
\[ g: \vec{x} = \vec{OP} + s \cdot \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix} \]
und
\[ h: \vec{x} = \vec{OQ} + t \cdot \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix} \]
mit \( s, t \in \mathbb{R} \).
a) Zeigen Sie, dass \( g \) und \( h \) nicht identisch sind.
b) Bestimmen Sie eine Gleichung der Gerade, die parallel zu \( g \) und \( h \) ist und die Strecke \( PQ \) im Punkt \( T \) schneidet, wobei \( 3 \cdot |PT| = |QT| \).
a) Zeigen Sie, dass \( g \) und \( h \) nicht identisch sind.
Zwei Geraden sind identisch, wenn sie denselben Stützvektor und denselben Richtungsvektor haben oder wenn ein Punkt von einer Geraden auch auf der anderen Geraden liegt.
Hier haben beide Geraden den gleichen Richtungsvektor \( \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix} \).
Der Stützvektor von \( g \) ist \( \vec{OP} \), welcher dem Punkt \( P(2 | 0 | 1) \) entspricht, und der Stützvektor von \( h \) ist \( \vec{OQ} \), welcher dem Punkt \( Q(2 | 4 | 9) \) entspricht.
Da \( P \) und \( Q \) verschiedene Punkte sind, haben die beiden Geraden unterschiedliche Stützvektoren.
Antwort a)
Die Geraden \( g \) und \( h \) sind nicht identisch, da sie unterschiedliche Stützvektoren haben.
b) Bestimmen Sie eine Gleichung der Gerade, die parallel zu \( g \) und \( h \) ist und die Strecke \( PQ \) im Punkt \( T \) schneidet, wobei \( 3 \cdot |PT| = |QT| \).
Da die Gerade parallel zu \( g \) und \( h \) sein soll, hat sie denselben Richtungsvektor \( \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix} \).
Die Strecke \( PQ \) lässt sich beschreiben als:
\[ \vec{x} = \vec{OP} + r \cdot (\vec{OQ} - \vec{OP}) \]
mit \( r \in [0,1] \).
Wegen \( 3 \cdot |PT| = |QT| \) und \( |PQ| = |PT| + |QT| \) ergibt sich:
\[ r = \frac{|PT|}{|PQ|} = \frac{1}{4} \]
Setzen Sie \( r = \frac{1}{4} \) in die Gleichung für die Strecke \( PQ \) ein, um den Punkt \( T \) zu finden.
Die Gleichung der gesuchten Geraden ist:
\[ \vec{x} = \vec{OT} + u \cdot \begin{pmatrix} 3 \\ -1 \\ 2 \end{pmatrix} \]
wobei \( \vec{OT} \) dem gefundenen Punkt \( T \) entspricht und \( u \in \mathbb{R} \).
Um den Punkt \( T \) zu finden, nutzen wir die gegebene Information über das Verhältnis zwischen den Strecken \( PT \) und \( QT \).
Da die gesamte Strecke \( PQ \) in vier gleiche Teile geteilt wird (drei Teile für \( PT \) und ein Teil für \( QT \)), entspricht dies einem Verhältnis von \( r = \frac{1}{4} \).
Bestimmung des Punktes \( T \) auf der Strecke \( PQ \):
- Der Ortsvektor von Punkt \( P \) ist \( \vec{OP} = \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} \) und von Punkt \( Q \) ist \( \vec{OQ} = \begin{pmatrix} 2 \\ 4 \\ 9 \end{pmatrix} \).
Die Gerade \( PQ \) kann als Verbindung zwischen diesen beiden Punkten beschrieben werden:
\[ \vec{x} = \vec{OP} + r \cdot (\vec{OQ} - \vec{OP}) \]
Setzen Sie \( r = \frac{1}{4} \) in die obige Gleichung ein:
\[ \vec{OT} = \vec{OP} + \frac{1}{4} \cdot (\vec{OQ} - \vec{OP}) \]
\[ \vec{OT} = \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} + \frac{1}{4} \cdot \left( \begin{pmatrix} 2 \\ 4 \\ 9 \end{pmatrix} - \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} \right) \]
\[ \vec{OT} = \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} + \frac{1}{4} \cdot \begin{pmatrix} 0 \\ 4 \\ 8 \end{pmatrix} \]
\[ \vec{OT} = \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} \]
Daher ist der Punkt \( T \) gegeben durch die Koordinaten \( T(2 | 1 | 3) \).
References
- The 7 Most Useful Data Analysis Techniques [2025 Guide] Avaliable at: The 7 Most Useful Data Analysis Techniques [2025 Guide]
- Data Analysis: Techniques, Tools, and Processes | IxDF Avaliable at: Data Analysis: Techniques, Tools, and Processes | IxDF
- Data Analysis Methods: Qualitative vs. Quantitative Techniques Avaliable at: Data Analysis Methods: Qualitative vs. Quantitative Techniques
- What Is Data Analysis: Examples, Types, & Applications Avaliable at: What Is Data Analysis: Examples, Types, & Applications
- Patrick S. Medina, R. W. Doerge (2016). Statistical Methods in Topological Data Analysis for Complex, High-Dimensional Data. Available at: http://arxiv.org/abs/1607.05150v1 (Accessed: 10 April 2025).
- Karen Kafadar (2012). Special section: Statistical methods for next-generation gene sequencing data. Available at: http://arxiv.org/abs/1206.6617v1 (Accessed: 10 April 2025).
- Boris Ryabko, Andrey Guskov, Irina Selivanova (2017). Using data-compressors for statistical analysis of problems on homogeneity testing and classification. Available at: http://arxiv.org/abs/1701.04028v1 (Accessed: 10 April 2025).










