Tangente: Definition, Berechnung & Formel

Q: Wie berechnet man die Tangente?

Die Tangente wird mit der Formel t(x)=f(x 0 )+f'(x 0 )(x-x 0 ) berechnet.

Springe zu einem wichtigen Kapitel

Tangente – Definition

Eine Tangente ist eine besondere Gerade, deren Name sich nicht zufällig von genau diesem lateinischen Wort herleiten lässt:

Eine Tangente ist eine Gerade, die eine Kurve oder eine geometrische Figur in einem Punkt P berührt. Berühren meint in diesem Falle, dass die Tangente und die Kurve/die Figur den Punkt P gemeinsam haben, die Tangente die Kurve/die Figur jedoch nicht schneidet.

Tangenten gibt es im Koordinatensystem (in der Analysis), aber auch in der Geometrie. In der Geometrie konstruiert man sie an verschiedene Figuren, zum Beispiel an Kreise oder Ellipsen. Wenn es um Tangenten im Koordinatensystem geht, ist man nicht nur daran interessiert Tangenten zu zeichnen, sondern auch sie zu berechnen.

Neben der Tangente gibt es noch zwei andere besondere Geraden, die in diesem Zusammenhang gemeinsam genannt werden. Diese sind die Sekante und die Passante.

Die Sekante ist eine Gerade, die eine Kurve oder eine Figur schneidet.
Die Passante ist eine Gerade, die eine Kurve oder eine Figur weder berührt, noch schneidet, also daran vorbeiläuft.

In dieser Abbildung siehst du diese drei besonderen Geraden an einer Kurve.

Tangente Tangente Sekante Passante StudySmarter Abbildung 1: Tangente, Sekante und Passante an einer Kurve

In diesem Artikel geht es um die Tangente als funktionale Gerade, also im Koordinatensystem.

Möchtest du die Tangente im Bereich der Geometrie genauer anschauen, speziell im Zusammenhang mit Kreisen, dann schaue dir den Artikel Geraden am Kreis an.

Die Tangente als funktionale Gerade

Für die ebene Geometrie – also die Geometrie im zweidimensionalen – reicht die Definition aus dem letzten Abschnitt aus. In der Analysis, also beim Betrachten von Tangenten an Kurven oder Funktionsgrafen, nutzt man meistens eine andere Definition der Tangente:

Die Tangente ist die Funktion role="math" $t (x)$ , die eine Funktion role="math" $f (x)$ in einem Punkt role="math" $P (x_{0} f (x_{0}))$ berührt und berechnet sich mit:

$t (x) = f (x_{0}) + f' (x_{0}) \cdot (x - x_{0})$

Man betrachtet also für die Tangente nur einen Punkt der Funktion und nicht die gesamte Funktion. Dadurch sehen Tangenten zum Teil anders aus, als man es sich aus der Geometrie herleiten würde, d. h. manchmal schneiden Tangenten den Graphen der anderen Funktion doch.

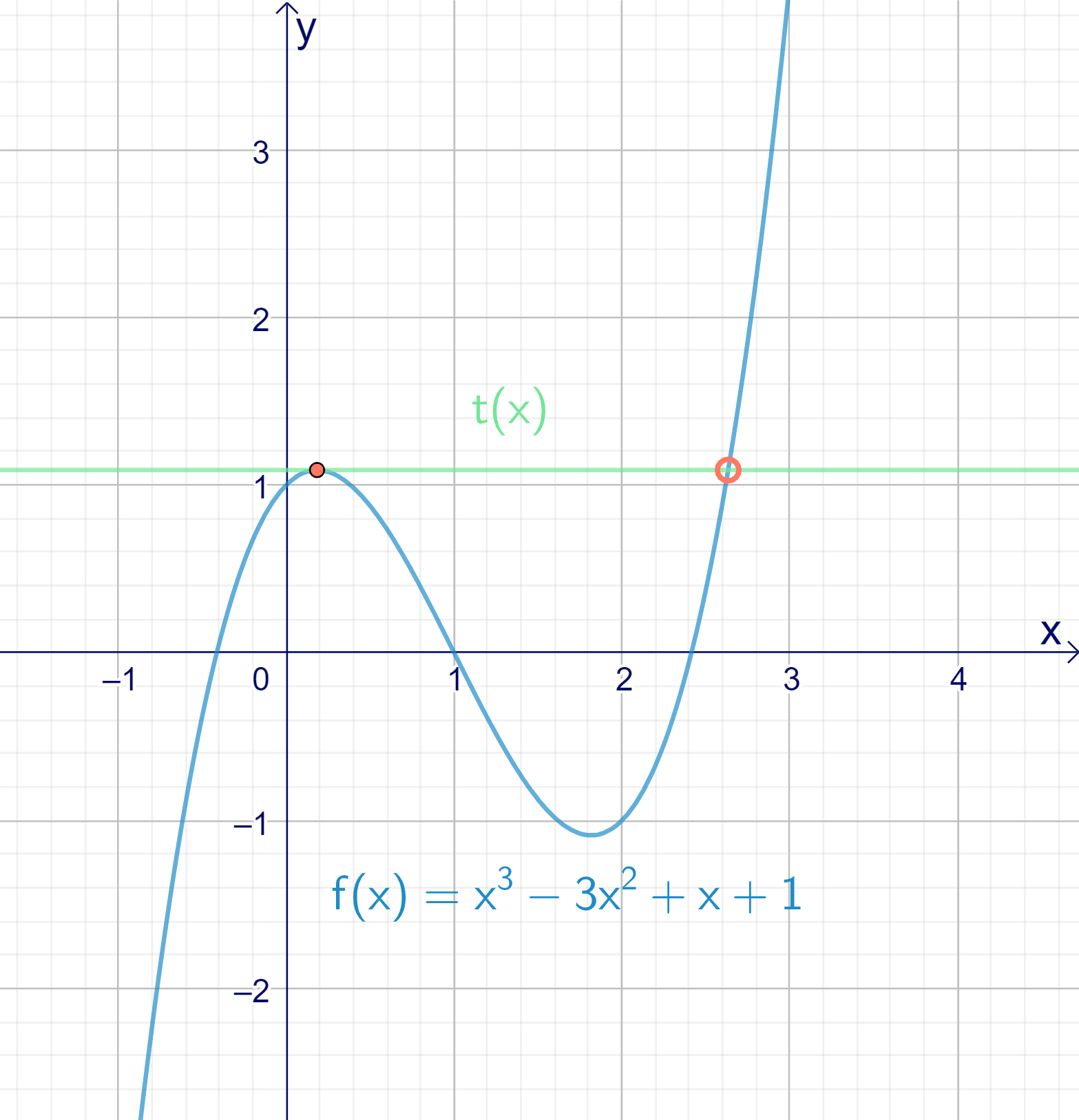
Tangente Tangente als funktionale Gerade StudySmarter

Abbildung 2: Tangente, die den Funktionsgraf schneidet

In Abbildung 2 siehst du eine Tangente, die den Graphen an einer Stelle weiter rechts schneidet. Diese Gerade ist trotzdem eine Tangente. Tangenten in der Analysis dürfen also den Graphen schneiden.

Das folgende Beispiel einer Tangente ist noch ungewöhnlicher, denn die Tangente schneidet den Graphen sogar an dem Punkt, an dem sie ihn berühren soll. Dennoch handelt es sich hierbei um eine Tangente.

Tangente Tangente als funktionale Gerade StudySmarter Abbildung 3: Tangente, die den Funktionsgraf schneidet

Du musst dir also zunächst folgendes merken: Eine Tangente in der Analysis ist nicht mehr wie in der Geometrie eine Gerade, die eine Figur nur in genau einem Punkt berührt. Tangenten in der Analysis können den Graphen auch schneiden, entweder in einem anderen Punkt als dem Berührpunkt, oder sogar direkt im Berührpunkt.

Weshalb ist das so?

Dazu wird ein bisschen ausgeholt: Da Tangenten Geraden sind, weisen sie alle Eigenschaften von linearen Funktionen auf.

Jede Tangente ist eine lineare Funktion der Form $t (x) = m x + t$ , wobei m die Steigung und t der y-Achsenabschnitt sind.

Besonders interessant an der Tangente ist ihre Steigung. Wird nun eine Tangente an eine Kurve gelegt, so gibt es einen wichtigen Punkt in Bezug auf die Steigung zu sagen: Im Berührpunkt P sind die Steigung der Tangente und die Steigung der Kurve identisch.

Da die Tangente eine lineare Funktion ist, bleibt ihre Steigung immer gleich. Bei anderen Funktionen ändert sich die Steigung aber, sodass es zu Schnittpunkten zwischen Tangente und Funktion kommen kann.

Man kann also sagen:

Die Tangente t in einem Punkt P zu einer Funktion f ist diejenige Gerade, die dieselbe Steigung hat wie die Funktion f im Punkt P.

Wenn du dir nochmal die beiden Abbildungen anschaust, kannst du sehen: Die Tangente in Abbildung 2 hat die Steigung 0, denn sie liegt an einem Extrempunkt der Funktion f, und dort ist die Steigung 0. Die Tangente in Abbildung 3 schneidet die Funktion f deshalb, weil die Funktion genau in f ihre Steigung ändert.

Man kann jedoch nicht an jedem Punkt eine Tangente finden. Das ist der Fall, wenn eine Funktion in einem Punkt keine eindeutige Steigung hat. Ein bekanntes Beispiel hierfür ist die Betragsfunktion.

Tangente Betragsfunktion StudySmarter Abbildung 4: Betragsfunktion und ihre Tangente

Im Ursprung hat die Funktion keine eindeutige Steigung. Deshalb gibt es auch keine eindeutige Tangente. Auf diese Problematik wird weiter unten im Artikel nochmal eingegangen.

Tangente berechnen – Formel

Als Nächstes geht es um die Berechnung der Tangente. Dafür benötigst du die Definition der Tangente:

$t (x) = f (x_{0}) + f' (x_{0}) \cdot (x - x_{0})$

Willst du nun die Tangente zu einer gegebenen Funktion f in einem bestimmten Punkt berechnen, musst du folgende Rechnungen durchführen:

Berechne die Ableitung f' der Funktion f.
Setze den Wert $x_{0}$ in die Formel der Tangente ein.

Tangentengleichung berechnen und Tangentialpunkte bestimmen

Hier ein Beispiel, wie du die Tangentengleichung berechnen kannst.

Aufgabe 1

Berechne die Tangentengleichung zur Funktion $f (x) = x^{3}$ im Punkt $(1 | 1)$ .

Lösung

Schritt 1: Berechne die Ableitung f'.

$f' (x) = 3 x^{2}$

Schritt 2: Setze den Wert für x₀in die Tangentengleichung ein. x₀ist hier 1.

$\begin{array}{rcl} t (x) & = & f (1) + f' (1) \cdot (x - 1) \\ = & 1^{3} + 3 \cdot 1^{2} \cdot (x - 1) \\ = & 1 + 3 x - 3 \\ = & 3 x - 2 \end{array}$

Aufgabe 2

Gegeben ist die Funktion $f (x) = 0, 5 x^{2} + 1$ .

Bestimme die Tangenten an den folgenden Punkten:

$P_{1} (- 3 | f (- 3))$
$P_{2} (- 3 | f (- 2))$
$P_{3} (0 | f (0))$
$P_{4} (2 | f (2))$
$P_{5} (3 | f (3))$

Lösung

Schritt 1: Berechne die Ableitung der Funktion.

$f' (x) = x$

Schritt 2: Setze die x-Werte der Punkte jeweils in die Tangenten –Formel ein.

Zu P₁:

$\begin{array}{rcl} t_{1} (x) & = & f (- 3) + f' (- 3) \cdot (x - (- 3)) \\ = & 0, 5 \cdot {(- 3)}^{2} + 1 + (- 3) \cdot (x + 3) \\ = & - 3 x - 3, 5 \end{array}$

Zu P₂:

$\begin{array}{rcl} t_{2} (x) & = & f (- 2) + f' (- 2) \cdot (x - (- 2)) \\ = & 0, 5 \cdot {(- 2)}^{2} + 1 + (- 2) \cdot (x + 2) \\ = & - 2 x - 1 \end{array}$

Zu P₃:

$\begin{array}{rcl} t_{3} (x) & = & f (0) + f' (0) \cdot (x - 0) \\ = & 0, 5 \cdot {(0)}^{2} + 1 + (0) \cdot x \\ = & 1 \end{array}$

Zu P₄:

$\begin{array}{rcl} t_{4} (x) & = & f (2) + f' (2) \cdot (x - 2) \\ = & 0, 5 \cdot 2^{2} + 1 + 2 \cdot (x - 2) \\ = & 2 x - 1 \end{array}$

Zu P₅:

$\begin{array}{rcl} t_{5} (x) & = & f (3) + f' (3) \cdot (x - 3) \\ = & 0, 5 \cdot 3^{2} + 1 + 3 \cdot (x - 3) \\ = & 3 x - 3, 5 \end{array}$

Die Tangenten sehen dann so aus:

Tangente Tangentialpunkte StudySmarter Abbildung 5: Tangenten aus Aufgabe 2

Tangente – Das Problem mit der Tangentensteigung

Kommen wir hier auf die Problematik von vorher zurück. Es gibt auch Punkte an Funktionsgrafen, an denen du keine Tangente finden kannst. Das hängt mit der Steigung zusammen. Denn die Steigung m der Tangente ist nichts anderes, als die Ableitung der Funktion an der Stelle x₀.

In Aufgabe 1 wurde gerechnet:

$\begin{array}{rcl} t (x) & = & f (1) + f' (1) \cdot (x - 1) \\ = & 1^{3} + 3 \cdot 1^{2} \cdot (x - 1) \\ = & 1 + 3 x - 3 \\ = & 3 x - 2 \end{array}$

In der Rechnung ist die Ableitung an der Stelle $x_{0} = 1$ blau markiert. In der letzten Zeile siehst du, dass sie genau die Steigung der Tangente ausmacht.

Voraussetzung für die Tangente ist also, dass die Ableitung der Funktion f an der Stelle x₀ existiert. Existiert sie nicht, ist die Funktion f an der Stelle x₀ nicht differenzierbar, ("ableitbar"), also existiert auch keine Tangente.

Das ist auch das Problem der Betragsfunktion an der Stelle $x_{0} = 0$ . Sie ist dort nicht differenzierbar.

Aus diesem Grund sagt man auch beim Ableiten, dass die Ableitung die Steigung der Tangente ist. Wenn du dir nicht mehr sicher bist, wann eine Funktion differenzierbar ist, dann schau dir den Artikel Differenzierbarkeit an.

Steigungswinkel einer Tangente berechnen

Hast du eine Tangente berechnet, kannst du neben ihrer Steigung auch den Steigungswinkel berechnen. Dafür benötigst du den Tangens.

Der Steigungswinkel $β$ einer linearen Funktion f der Form $x \to m x + t$ lässt sich berechnen durch:

$β = \tan^{- 1} (m)$

Tipp: Wenn du ein negatives m hast, musst du $180 ° - β$ rechnen.

Der Steigungswinkel ist dabei der Winkel, der zwischen der linearen Funktion und der x-Achse eingeschlossen wird.

Tangente Steigungswinkel StudySmarter Abbildung 6: Steigungswinkel der 5. Tangente aus Aufgabe 2

Am folgenden Beispiel kannst du sehen, wie man einen Steigungswinkel konkret berechnet.

Aufgabe 3

Betrachte die Tangente aus Aufgabe 1 und berechne hier den Steigungswinkel.

Lösung

Die Tangente aus Aufgabe 1 war $t (x) = 3 x - 2$ . Ihre Steigung m ist also 3.

Mithilfe der Formel für den Steigungswinkel erhältst du:

$β = \tan^{- 1} (m) = \tan^{- 1} (3) = 71.57 °$

Tangente – Das Wichtigste

Eine Tangente ist eine Gerade, die eine Kurve oder eine geometrische Figur in einem Punkt P berührt.
Eine Tangente in der funktionalen Analysis ist eine Funktion t(x), die eine Funktion f(x) in einem Punkt P(x₀|f(x₀)) berührt. Sie berechnet sich mit $t (x) = f (x_{0}) + f' (x_{0}) \cdot (x - x_{0})$ .
Die Tangente t und die Funktion f haben dann im Punkt P dieselbe Steigung.
Die Tangente an einem Punkt einer gegebenen Funktion kann berechnet werden, indem man
- die Ableitung f' berechnet
- x₀ dann in die Tangentenformel einsetzt
Ist eine Funktion in einem Punkt nicht differenzierbar, so gibt es an diesem Punkt keine Tangente.
Der Steigungswinkel $β$ einer Tangente kann berechnet werden durch die Formel $β = \tan^{- 1} (m)$ , wobei m die Steigung der Tangente ist.

Karteikarten in Tangente 6

Lerne jetzt

Dürfen Tangenten in der Analysis Graphen schneiden?

Was gilt für jede Tangente?

Jede Tangente ist eine lineare Funktion.

Was passiert im Berührpunkt P mit der Steigung der Tangente und der Steigung der Kurve?

Im Berührpunkt P sind die Steigung der Tangente und die Steigung der Kurve identisch.

Wo gibt es Tangenten?

In der Analysis

Welche besonderen Geraden gibt es?

Passante

Was ist eine Voraussetzung für eine Tangente?

Die Ableitung der Funktion f an der Stelle x₀ muss existieren.

Mit E-Mail registrieren

Du hast bereits ein Konto? Anmelden

Häufig gestellte Fragen zum Thema Tangente

Was ist die Tangente einer Funktion?

Eine Tangente t(x) ist eine lineare Funktion, welche eine andere Funktion f(x) in einem Punkt P (x₀|fx₀)) berührt. Sie berechnet sich mit der Formel t(x)=f(x₀)+f'(x₀)(x-x₀)

Wie findet man eine Tangente?

Die Tangente findet man, indem die Tangentenformel t(x)=f(x₀)+f'(x₀)(x-x₀) angewendet wird.

Dafür leitet man die Funktion f ab und setzt den Wert x₀ in Ausgansfunktion sowie in die Ableitung ein und das alles wiederum in die Formel. Dadurch erhält man die Gleichung der Tangente.

Was ist der Unterschied zwischen einer Sekante und einer Tangente?

Eine Tangente berührt die Funktion in einem Punkt. Eine Sekante hat mehrere Schnittpunkte mit der Funktion.

Wie berechnet man die Tangente?

Die Tangente wird mit der Formel t(x)=f(x₀)+f'(x₀)(x-x₀) berechnet.

Erklärung speichern

Teste dein Wissen mit Multiple-Choice-Karteikarten

Punktzahl

Greife auf über 700 Millionen Lernmaterialien zu

Lerne effizienter mit Karteikarten

Erziele bessere Noten mit AI

Hast du bereits ein Konto? Logge dich ein

Weiter

Entdecke Lernmaterialien mit der kostenlosen StudySmarter App

Kostenlos anmelden

Über StudySmarter

StudySmarter ist ein weltweit anerkanntes Bildungstechnologie-Unternehmen, das eine ganzheitliche Lernplattform für Schüler und Studenten aller Altersstufen und Bildungsniveaus bietet. Unsere Plattform unterstützt das Lernen in einer breiten Palette von Fächern, einschließlich MINT, Sozialwissenschaften und Sprachen, und hilft den Schülern auch, weltweit verschiedene Tests und Prüfungen wie GCSE, A Level, SAT, ACT, Abitur und mehr erfolgreich zu meistern. Wir bieten eine umfangreiche Bibliothek von Lernmaterialien, einschließlich interaktiver Karteikarten, umfassender Lehrbuchlösungen und detaillierter Erklärungen. Die fortschrittliche Technologie und Werkzeuge, die wir zur Verfügung stellen, helfen Schülern, ihre eigenen Lernmaterialien zu erstellen. Die Inhalte von StudySmarter sind nicht nur von Experten geprüft, sondern werden auch regelmäßig aktualisiert, um Genauigkeit und Relevanz zu gewährleisten.

Erfahre mehr

StudySmarter Redaktionsteam

Team Mathe Lehrer

8 Minuten Lesezeit
Geprüft vom StudySmarter Redaktionsteam

Erklärung speichern

Tangente

StudySmarter Redaktionsteam

Tangente – Definition