Während einer Kurvendiskussion untersuchst Du bestimmte Punkte einer Funktion. Ein spezieller Punkt ist dabei der Wendepunkt, durch den die sogenannte Wendetangente verläuft und dabei die Steigung des Wendepunktes angibt.
Was ein Wendepunkt ist, wie die Tangente im Wendepunkt bestimmt wird und wie Du die Wendetangente einzeichnen kannst, lernst Du in dieser Erklärung. Außerdem findest Du am Ende noch einige Aufgaben zur Bestimmung der Wendetangente.
Wendetangente berechnen – Grundlagen
Bevor Du Dich genauer mit der Wendetangente auseinandersetzt, solltest Du wissen, was Funktionen sind, wie Du sie ableitest und worum es sich bei Tangenten handelt.
Zur Erinnerung: Tangenten sind Geraden, die, wie der Name schon sagt, Funktionen in einem Punkt berühren und die Steigung in diesem Punkt darstellen.
Alles Weitere zu diesen Themen erfährst Du in den folgenden Erklärungen:
Wendetangente berechnen – Tangente im Wendepunkt
Wie der Name also schon sagt, ist die Wendetangente die Tangente einer Funktion in ihrem Wendepunkt.
Der Wendepunkt \(W\) einer Funktion ist der Punkt im Graphen, in dem sich das Krümmungsverhalten der Funktion ändert. Das bedeutet, der Wendepunkt liegt dort, wo der Graph von einer Rechtskurve in eine Linkskurve wechselt oder umgekehrt.
Gleichung der Wendetangente
Da die Tangente eine lineare Funktion ist, gibt es eine Funktionsgleichung für die Wendetangente.
Die Wendetangente \(t\) ist die Tangente einer Funktion \(f(x)\) in ihrem Wendepunkt \(W(x_w|f(x_w))\).
Dabei handelt es sich um eine lineare Funktion der Form \[y=mx+b\], wobei \(m\) die Steigung an der Wendestelle beschreibt.
Ein Beispiel für die Wendetangente \(t\) siehst Du nachfolgend am Beispiel.
Gegeben ist die Funktion \(f(x)=x^3-4x^2\). Die Wendetangente am Wendepunkt \(W\) sieht dann wie folgt aus:
Abb. 1 – Wendetangente
Wendetangente berechnen mit Wendepunkt
Die Funktionsgleichung der Wendetangente setzt sich zusammen aus mehreren Komponenten. Grundlegend ist der Wendepunkt der erste Schritt, um die Wendetangente überhaupt berechnen zu können. Zudem braucht es für eine lineare Funktionsgleichung immer eine Steigung sowie einen y-Achsenabschnitt.
Hier erfährst Du alle Schritte, um die Gleichung der Wendetangente berechnen zu können.
1. Wendetangente Wendepunkt – Wendepunkt berechnen
Die Wendetangente ist also die Gerade, die die Funktion im Wendepunkt berührt.
Auf folgender Abbildung siehst Du den Graphen der Funktion \(f(x)=x^3\) sowie ihren Wendepunkt \(W(0|0)\).
Abb. 2 – Funktion mit Wendepunkt
Den Wendepunkt berechnest Du über die zweite und dritte Ableitung der Funktion. Wie das genau geht, erfährst Du in der Erklärung Wendepunkt berechnen. Außerdem findest Du hier eine kurze Anleitung mit einfachem Beispiel für die Funktion \(f(x)=3x^3\).
| Vorgehen | Beispiel |
| 1. Du leitest Deine gegebene Funktion dreimal ab. | \begin{align} f(x)&=3x^3 \\ f'(x)&=9x^2 \\ f''(x)&=18x \\ f'''(x)&=18\end{align} |
| 2. Notwendige Bedingung: Du prüfst, für welchen Wert die zweite Ableitung der Funktion gleich 0 ist. | \begin{align}f''(x)&=0 \\ \Leftrightarrow 18x&=0 \\ \Leftrightarrow x&=0 \end{align} |
| 3. Hinreichende Bedingung: Du prüfst, ob die dritte Ableitung ungleich 0 ist. | \[f'''(x)=18 \neq 0\] |
| 4. Du berechnest den passenden y-Wert, indem Du den in 2. gefundenen x-Wert in f(x) einsetzt. | \[f(0)=3\cdot 0^3=0\] \[\Rightarrow W(0|0)\] |
2. Wendetangente Steigung – Steigung der Wendetangente berechnen
Die Steigung der Wendetangente kann ebenfalls berechnet werden.
Die Steigung \(m\) der Wendetangente entspricht der Steigung der Funktion \(f\) im Wendepunkt \(W\). Sie wird dementsprechend berechnet mit der ersten Ableitung der Funktion: \[f'(x_w).\]
Anhand des folgenden Beispiels kannst Du Dir einmal konkret ansehen, wie so eine Steigung berechnet wird.
Gegeben ist die Funktion \(f(x)=x^3-3x^2\) mit Wendepunkt \(W(1|-2)\).
Um die Steigung zu berechnen, wird die erste Ableitung benötigt: \[f'(x)=3x^2-6x\]
Dann kann der x-Wert des Wendepunkts in die erste Ableitung eingesetzt werden: \[f'(1)=3\cdot 1^2-6\cdot 1 =-3\]
Das Ergebnis ist dann die Steigung, hier also \[m=-3\]
Nun kennst Du die Steigung \(m\) der Tangente. Um die Wendetangente einzeichnen zu können, hilft es, ihren y-Achsenabschnitt zu kennen. Dieser ist ein wichtiger Bestandteil der Funktionsgleichung.
3. Wendetangente y-Achsenabschnitt berechnen
Bisher kennst Du den Wendepunkt \(W\) und die Steigung \(m\). Es fehlt also noch der y-Achsenabschnitt \(b\). Um ihn zu berechnen, setzt Du alle bisher bekannten Werte in eine allgemeine lineare Funktionsgleichung \(y=mx+b\) ein und stellst nach \(b\) um. Hast Du \(b\) herausgefunden, kannst Du die Tangentengleichung der Wendetangente aufstellen.
Gegeben ist wieder die Funktion \(f(x)=x^3-3x^2\) mit Wendepunkt \(W(1|-2)\) und Steigung \(m=-3\).
Setze nun alle bisher bekannten Werte in eine allgemeine lineare Funktionsgleichung \(y=mx+b\) ein: \[-2=-3\cdot1+b\] Formst Du nach \(b\) um, erhältst Du
\[b=1\]
Die Funktionsgleichung der Wendetangente lautet dann \[t_w(x)=-3x+1\]
Wendetangente berechnen – Wendenormale
Kennst Du die Funktionsgleichung der Wendetangente, kannst Du recht schnell die Gleichung der Wendenormale berechnen.
Die Wendenormale \(n\) ist eine lineare Funktion, die senkrecht zur Wendetangenten durch den Wendepunkt verläuft.
Die Wendenormale n kann berechnet werden mittels der Gleichung \[n_w(x)=-\frac{1}{f'(x_w)}\cdot (x-x_w)+f(x_w).\]
Du kannst Dir die Wendenormale also so vorstellen, dass sie eine um \(90^\circ\) gedrehte Wendetangente ist. Der Wendepunkt ist dabei der Drehpunkt.
Abb. 3 – Wendenormale
Wendetangente einzeichnen
Da die Wendetangente eine lineare Funktion ist, kannst Du sie mithilfe eines Lineals oder Geodreiecks einzeichnen. Du benötigst dafür den Wendepunkt einer Funktion \(f(x)\).
Wichtig ist, dass Du weißt, wie Du ein Steigungsdreieck einzeichnest. Wie das geht, erfährst Du z. B. in der Erklärung Graphen zeichnen. Dann gehst Du wie folgt vor:
| Vorgehen | Beispiel |
1. Zeichne den Wendepunkt in die Funktion ein. | Gegeben ist \(f(x)=x^3-3x^2\).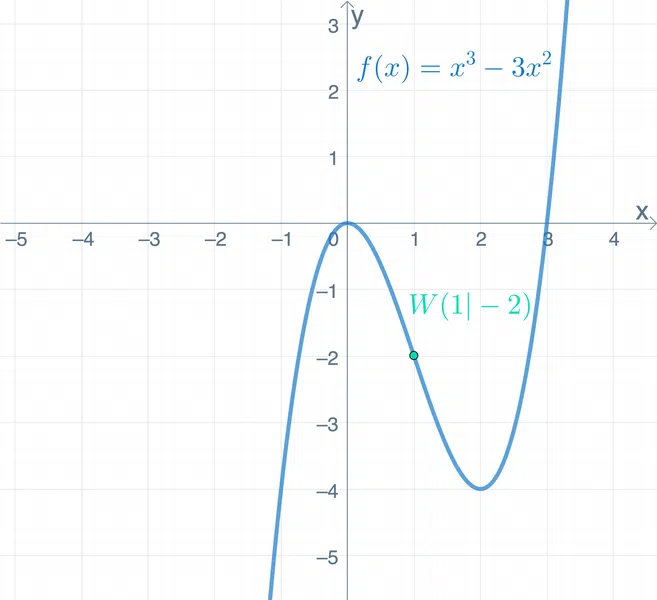 
|
2. Zeichne ein Steigungsdreieck für die Steigung \(m\) der Wendetangente an den Wendepunkt. Daraus ergibt sich eine Steigung von \(m=-3\). | Die Steigung ist hier m=-3.  |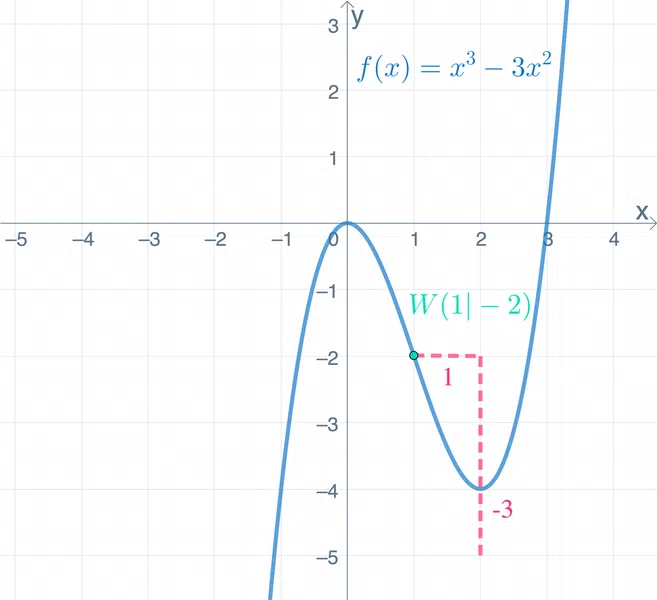
3. Verbinde die Spitze des Steigungsdreiecks mit dem Wendepunkt \(W\). |  |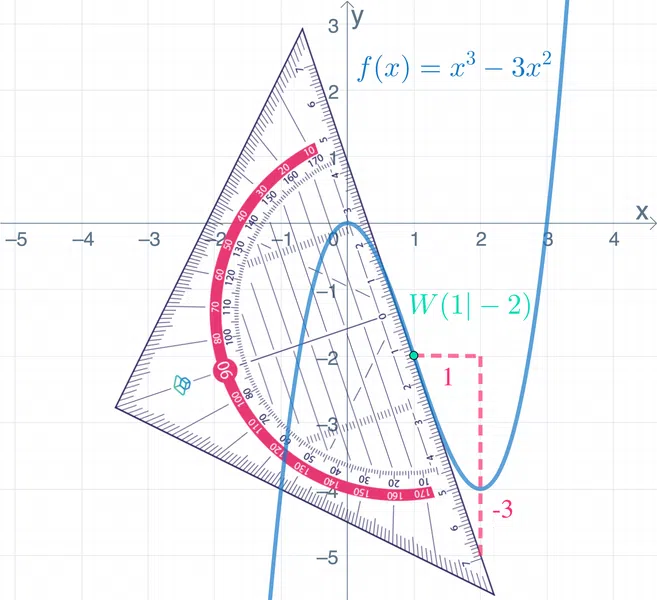
4. Die Gerade, die Du erhältst, ist die Wendetangente \(t\). Hier kannst Du nun den entsprechenden y-Achsenabschnitt, also den Schnittpunkt der Wendetangente mit der y-Achse bei \(b=1\), ablesen. Mit der Steigung und dem y-Achsenabschnitt kannst Du nun auch die Funktionsgleichung der Wendetangente bilden. \[\rightarrow y=-3x+1\] |  |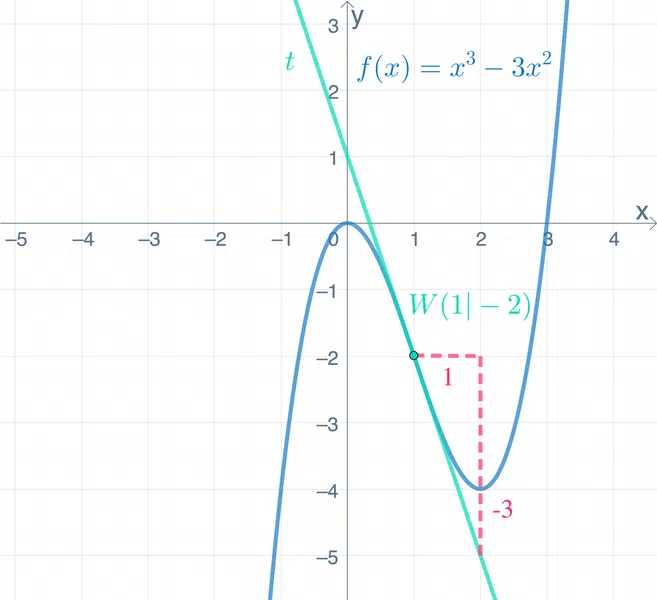
Wendetangente e Funktion
Bisher konntest Du hier nur Beispiele für Wendetangenten ganzrationaler Funktionen ansehen. Doch wie ist das bei komplexeren Funktionen, z. B. bei der e-Funktion?
Eine e-Funktion besitzt nur dann Wendepunkte, wenn sie mit einer ganzrationalen Funktion verknüpft ist, die mindestens den Grad 2 besitzt. Nur dann existiert auch eine Wendetangente.
Das liegt daran, dass die e-Funktion allein nie 0 wird, auch nicht ihre Ableitungen.
Somit kann die notwendige Bedingung für Wendepunkte nur angewandt werden, wenn die zweite Ableitung eine Nullstelle besitzt.
Für die Funktion \(f(x)=e^{x}-x^2\) existieren Wendepunkte, da sie mit der ganzrationalen Funktion \(x^2\) verknüpft ist. Somit kann auch eine Wendetangente \(t\) bestimmt werden.
Abb. 8 – Wendetangente einer e-Funktion
Für die Funktion \(f(x)=e^{x}-2\) existieren keine Wendepunkte. Demnach kann auch keine Wendetangente bestimmt werden.
Wie Du eine e-Funktion ableitest und mehr erfährst Du in der Erklärung e Funktion ableiten.
Wendetangente Steckbriefaufgaben
In Steckbriefaufgaben kann es vorkommen, dass Du eine Wendetangente gegeben hast. Dieser kannst Du Informationen entnehmen, die für das Aufstellen der gesuchten Funktion wichtig sind.
Eine gegebene Funktionsgleichung \(t_w=mx+b\) der Wendetangente gibt Dir folgende Informationen für die gesuchte Funktion \(f\):
- Die erste Ableitung von \(f\) besitzt im x-Wert des Wendepunkts die Steigung \(m\): \[f'(x_w)=m.\]
- Bei gegebener Wendestelle \(x_w\) kannst Du mithilfe der Wendetangente den passenden y-Wert herausfinden: \[f(x_w)=t(x_w)=mx_w+b.\]
In den folgenden Aufgaben findest Du einen Teil einer Steckbriefaufgabe, an der Du die Anwendung üben kannst.
Wendetangente berechnen – Aufgaben
Da Du nun einiges über Wendetangenten und ihre Berechnung lernen konntest, kannst Du Dein Wissen anhand der folgenden Aufgaben testen.
Aufgabe 1
Sieh Dir die folgende Abbildung an. Welche der eingezeichneten Geraden ist die Wendetangente an die Funktion \(f\)?
Abb. 9 – Aufgabe 1
Lösung
Die Gerade \(i\) verläuft nicht durch einen Wendepunkt, da an der Stelle, an der sie die Funktion berührt, kein Kurvenwechsel stattfindet.
Die Gerade \(h\) verläuft zwar durch den Wendepunkt, allerdings verläuft sie senkrecht zur eigentlichen Wendetangente.
Gerade \(g\) verläuft durch den Wendepunkt und besitzt die gleiche Steigung wie die Funktion in diesem Punkt. Daher ist sie die Wendetangente.
Aufgabe 2
Gegeben ist die Funktion \(f(x)=x^3+2x-1\). Bestimme die Funktionsgleichung ihrer Wendetangente.
Lösung
Zunächst bestimmst Du den Wendepunkt der Funktion. Dafür benötigst Du die zweite und dritte Ableitung: \begin{align} f(x)&=x^3+2x-1\\ f'(x)&=3x^2+2 \\ f''(x))&=6x \\ f'''(x)&=6 \end{align}
Dann nutzt Du die notwendige Bedingung und setzt die zweite Ableitung gleich 0:
\begin{align} f''(x)&=0 \\ \Leftrightarrow 6x&=0 \\ \Leftrightarrow x&=0 \end{align}
Mit der hinreichenden Bedingung prüfst Du, ob \(f'''(x)\) an der Wendestelle ungleich 0 ist. Dies ist der Fall, da \(f'''(x)\) konstant den Wert 6 besitzt.
Nun kennst Du die Wendestelle und kannst den passenden Funktionswert herausfinden, indem Du sie in die Funktion f einsetzt: \[f(0)=0^3+2 \cdot 0-1=-1.\]
Der Wendepunkt lautet also \(W(0|-1)\).
Als nächstes berechnest Du die Steigung \(m\) mithilfe der Wendestelle und der ersten Ableitung: \begin{align} m&=f'(x_w) \\[0.1cm] &= f'(0)\\[0.1cm] &= (3\cdot 0^2+2)\\[0.1cm] &=2 .\end{align}
Dann setzt Du m und den Wendepunkt in die allgemeine lineare Funktionsgleichung ein und löst nach \(b\) auf:
\begin{align} y&=mx+b \\[0.1cm] \Rightarrow -1&=2\cdot0+b \\[0.1cm] \Leftrightarrow -1&=b.\end{align}
Die Gleichung der Wendetangente lautet also \[t_w(x)=2x-1\].
Aufgabe 3
Gegeben ist eine Wendetangente \(t_w(x)=\dfrac{1}{2}x-\dfrac{3}{4}\) und ein Wendepunkt \(W(3|f(3))\) einer Funktion \(f\). Welche Hinweise kannst Du daraus auf die Funktion \(f\) schließen?
Lösung
Die Steigung der Funktion f an der Stelle \(x=3\) entspricht der Steigung \(m\) der Wendetangente an dieser Stelle. Somit gilt: \[f'(3)=m=\frac{1}{2}.\]
Außerdem kann der passende Funktionswert des Wendepunkts mithilfe der Wendetangente berechnet werden: \[f(3)=t(3)=\frac{1}{2}\cdot 3-\frac{3}{4}=1,5-0,75=0,75.\]
Der Wendepunkt lautet also \(W(3|0,75)\).
Wendetangente berechnen – Das Wichtigste
- Die Wendetangente \(t\) ist die Tangente einer Funktion \(f(x)\) in ihrem Wendepunkt \(W(x_w|f(x_w))\). Dabei handelt es sich um eine lineare Funktion der Form \[y=mx+b\], wobei \(m\) die Steigung an der Wendestelle beschreibt.
- Der Wendepunkt \(W\) einer Funktion ist der Punkt im Graphen, in dem sich das Krümmungsverhalten der Funktion ändert.
- Den Wendepunkt berechnest Du wie folgt:
- Funktion \(f\) dreimal ableiten.
- Zweite Ableitung gleich 0 setzen und nach \(x\) auflösen.
- Herausgefundenen Wert in die dritte Ableitung einsetzen und prüfen, ob der Wert ungleich 0 ist. Nur dann liegt eine Wendestelle vor.
- Wendestelle für \(x\) in \(f\) einsetzen und damit den zugehörigen Funktionswert ermitteln.
- Die Steigung \(m\) der Wendetangente entspricht der Steigung der Funktion \(f\) im Wendepunkt \(W\). Sie wird dementsprechend berechnet mit \[f'(x_w).\]
- Den y-Achsenabschnitt berechnest Du, indem Du den Wendepunkt in die allgemeine Funktionsgleichung einsetzt und nach \(b\) auflöst.
- Da die Wendetangente eine lineare Funktion ist, kannst Du sie mithilfe eines Lineals oder Geodreiecks einzeichnen. Dafür zeichnest Du ein Steigungsdreieck an den Wendepunkt und verbindest ihn mit der Dreiecksspitze.
- Eine e-Funktion besitzt nur dann Wendepunkte, wenn sie mit einer ganzrationalen Funktion verknüpft ist, die mindestens den Grad 2 besitzt.
- Bei Steckbriefaufgaben kannst Du bei gegebener Wendestelle \(x_w\) und Wendetangente \(t_w(x)=mx+b\) Folgendes über die Funktion \(f\) entnehmen:
- Die Steigungen im Wendepunkt stimmen überein: \[f'(x_w)=m.\]
- Du kannst den passenden Funktionswert zur Wendestelle bestimmen: \[f(x_w)=t(x_w)=mx_w+b.\]
Nachweise
- Pfeffer (2013). Analysis für Fachoberschulen: Ein Lehr- und Arbeitsbuch zur modernen Mathematik. Springer-Verlag.
Erklärungen 
Magazine 
