Abstand paralleler Ebenen: Berechnen, Aufgaben & Formel

Springe zu einem wichtigen Kapitel

Mathematisch kannst Du Dir nun vorstellen, dass der Fußboden in einer Ebene liegt. Parallel dazu liegt die Decke in einer zweiten Ebene. Dein gemessener Abstand ist genau der Abstand dieser parallelen Ebenen.

Jetzt ist es leider nicht möglich, immer den Abstand zwischen zwei Ebenen zum Beispiel mit einem Maßband auszumessen. Deswegen gibt es Rechenverfahren, mit denen Du den Abstand zwischen zwei parallelen Ebenen berechnen kannst.

Abstand paralleler Ebenen – Ebenengleichungen: Parameterform, Normalenform, Koordinatenform

Bevor Du mit den Rechenverfahren zur Abstandsberechnung starten kannst, solltest Du ein paar Grundbegriffe und Rechnungen kennen. Diese werden in diesem Abschnitt kurz wiederholt. Wenn Du dich hier schon gut auskennt, kannst Du auch gleich zum nächsten Abschnitt springen.

Aus Sicht der Mathematik ist eine Ebene eine gerade Fläche, die unbegrenzt ist. Eine Ebene ist durch drei Punkte eindeutig bestimmt. Stell Dir zum Beispiel ein Blatt Papier vor, das unendlich groß ist. Dann hast Du eine Ebene. Wenn Du jetzt drei Punkte des Blattes kennst, weißt Du genau, wie das unendliche Blatt im Raum liegt.

Abstand paralleler Ebenen Papier Ebene StudySmarter

Angenommen eine Ebene geht durch die Punkte $A, B$ und $C$ . Dann kannst Du mithilfe der Ortsvektoren dieser Punkte eine Ebenengleichung angeben. Dabei ist ein Ortsvektor der Stützvektor der Ebene. Mit den anderen Ortvektoren berechnest du die Richtungsvektoren und erhältst eine Ebenengleichung in Parameterform.

Für eine Ebene $E$ mit den Punkten $A, B, C$ ist die Ebenengleichung in Parameterform

$E : \vec{x} = \vec{O A} + r \cdot \vec{A B} + s \cdot \vec{A C}$

Wenn Du also drei Punkte einer Ebene hast, kannst du die Ebenengleichung in Parameterform berechnen.

Gegeben ist die Ebene $E_{1}$ mit den Punkten id="2640452" role="math" $A = (1 | 2 | 3)$ , id="2640454" role="math" $B = (2 | 2 | 2)$ und id="2640465" role="math" $C = (2 | 3 | 1)$ . Mit diesen Punkten kannst du nun eine Ebenengleichung in Parameterform aufstellen. Die Ortsvektoren sind:

$\vec{O A} = (\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}), \vec{O B} = (\begin{matrix} 2 \\ 2 \\ 2 \end{matrix}), \vec{O C} = (\begin{matrix} 2 \\ 3 \\ 1 \end{matrix})$

Das Berechnen der Richtungsvektoren ergibt:

$\vec{A B} = (\begin{matrix} 2 - 1 \\ 2 - 2 \\ 2 - 3 \end{matrix}) = (\begin{matrix} 1 \\ 0 \\ - 1 \end{matrix}), \vec{A C} = (\begin{matrix} 2 - 1 \\ 3 - 2 \\ 1 - 3 \end{matrix}) = (\begin{matrix} 1 \\ 1 \\ - 2 \end{matrix})$

Dies kannst du jetzt in die Parameterform einsetzen und erhältst:

$E_{1} : \vec{x} = (\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) + s \cdot (\begin{matrix} 1 \\ 1 \\ - 2 \end{matrix})$

Die beiden Richtungsvektoren der Ebenengleichung in Parameterform müssen linear unabhängig sein.

Eventuell ist Dir bereits aufgefallen, dass die Ebenengleichungen nicht immer so aussehen wie in diesem Beispiel. Das liegt daran, dass es noch weitere Formen der Ebenengleichungen gibt.

Um den Abstand von parallelen Ebenen zu berechnen, benötigst Du auch die Normalenform sowie die Koordinatenform.

Um die Normalenform einer Ebene aufzustellen, berechnest Du einen Normalenvektor. Das ist ein Vektor der senkrecht zur Ebene steht. Dazu verwendest Du das Kreuzprodukt aus den beiden Richtungsvektoren.

Gegeben ist wieder die Ebene $E_{1}$ wie eben. Du berechnest das Kreuzprodukt der beiden Richtungsvektoren und bestimmst so einen Normalenvektor.

$\vec{n} = \vec{A B} \times \vec{A C} = (\begin{matrix} 1 \\ 0 \\ - 1 \end{matrix}) \times (\begin{matrix} 1 \\ 1 \\ - 2 \end{matrix}) = (\begin{matrix} 0 \cdot (- 2) - (- 1) \cdot 1 \\ (- 1) \cdot 1 - 1 \cdot (- 2) \\ 1 \cdot 1 - 0 \cdot 1 \end{matrix}) = (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix})$

Wenn du den Normalenvektor hast, kannst du die Ebenengleichung in Normalenform aufstellen.

Für eine Ebene $E$ mit Normalenvektor $\vec{n}$ und Stützvektor $\vec{p}$ ist die Ebenengleichung in Normalenform:

$E : [\vec{x} - \vec{p}] \circ \vec{n} = 0$

Mit dieser Definition kannst Du nun eine Ebenengleichung für das Beispiel aufstellen.

Mit dem ebenen berechnetem Normalenvektor und dem Ortsvektor $\vec{O A}$ als Stützvektor lautet die Ebenengleichung der Ebene $E_{1}$ :

$E_{1} : [\begin{matrix} \vec{x} - (\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}) \end{matrix}] \circ (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) = 0$

Von der Normalenform einer Ebenengleichung kannst du durch Ausrechnen des Skalarprodukt die Koordinatenform einer Ebenengleichung erhalten.

Die Koordinatenform einer Ebene $E$ ist

$E : a \cdot x_{1} + b \cdot x_{2} + c \cdot x_{3} = d$

Wie sieht also die Koordinatenform der Ebene aus dem Beispiel aus?

Du berechnest das Skalarprodukt aus der Normalenform.

$\begin{array}{rcl} [\begin{matrix} \vec{x} - (\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}) \end{matrix}] \circ (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) & = & 0 \\ (\begin{matrix} x_{1} - 1 \\ x_{2} - 2 \\ x_{3} - 3 \end{matrix}) \circ (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) & = & 0 \\ (x_{1} - 1) \cdot 1 + (x_{2} - 2) \cdot 1 + (x_{3} - 3) \cdot 1 & = & 0 \\ x_{1} - 1 + x_{2} - 2 + x_{3} - 3 & = & 0 \\ x_{1} + x_{2} + x_{3} - 6 & = & 0 \end{array}$

Die Koordinatenform den Ebenengleichung ist

$E_{1} : x_{1} + x_{2} + x_{3} = 6$

In der Koordinatenform sind die Faktoren vor den Koordinaten genau die Werte des Normalenvektors. Im Beispiel bestand der Normalenvektor nur aus Einsen. Deswegen stehen in der Koordinatenform keine Faktoren.

Diese Formen der Ebenengleichungen benötigst Du, um den Abstand zwischen parallelen Ebenen zu berechnen.

Abstand paralleler Ebenen – bestimmen

Aber wann sind Ebenen überhaupt parallel? Und wieso wird nur der Abstand von parallelen Ebenen berechnet?

Erinnere Dich an das Beispiel mit dem Fußboden und der Zimmerdecke aus dem Einstieg. Augenscheinlich kannst Du sagen, dass die Bodenebene und die Deckenebene parallel sind. Doch wie lässt sich das mathematisch überprüfen?

Um zu bestimmen, ob zwei Ebenen parallel sind, benötigst du die Ebenengleichungen am besten in Normalenform oder in Koordinatenform. Dann kannst Du den Normalenvektor direkt ablesen und überprüfen, ob sie kollinear, also voneinander abhängig, sind.

Gegeben sind die Ebenen $E_{2} : 2 \cdot x_{1} + 4 \cdot x_{2} + 2 \cdot x_{3} = 4$ und $E_{3} : [\begin{matrix} \vec{x} - (\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) \end{matrix}] \circ (\begin{matrix} 1 \\ 2 \\ 1 \end{matrix}) = 0$ .

Für die Ebene $E_{3}$ steht der Normalenvektor in der Ebenengleichung. Es ist $\vec{n_{3}} = (\begin{matrix} 1 \\ 2 \\ 1 \end{matrix})$ . Für die Ebene $E_{2}$ kannst Du den Normalenvektor aus den Faktoren vor den Koordinaten ablesen. Der Normalenvektor ist $\vec{n_{2}} = (\begin{matrix} 2 \\ 4 \\ 2 \end{matrix})$ .

Nun musst du überprüfen, ob die Normalenvektoren kollinear sind. Ist dies der Fall, sind die Ebenen parallel oder identisch. Im Beispiel ist $\vec{n_{2}} = 2 \cdot n_{3}$ . Die Normalenvektoren sind also kollinear. Jetzt könnten die Ebenen noch identisch sein. Um dies zu überprüfen, kannst du zum Beispiel den Punkt $(1 / 3 / 1)$ von $E_{3}$ in die Koordinatengleichung von $E_{2}$ einsetzen.

$2 \cdot 1 + 4 \cdot 3 + 2 \cdot 1 = 2 + 12 + 2 = 16$

Damit der Punkt aber auch in $E_{2}$ liegt, müsste die Summe aber 4 sein. Der Punkt liegt also nicht in $E_{2}$ . Die Ebenen sind nicht identisch, sondern parallel. Die kannst Du auch gut in Abbildung 1 sehen. Dort sind die beiden Ebenen dargestellt.

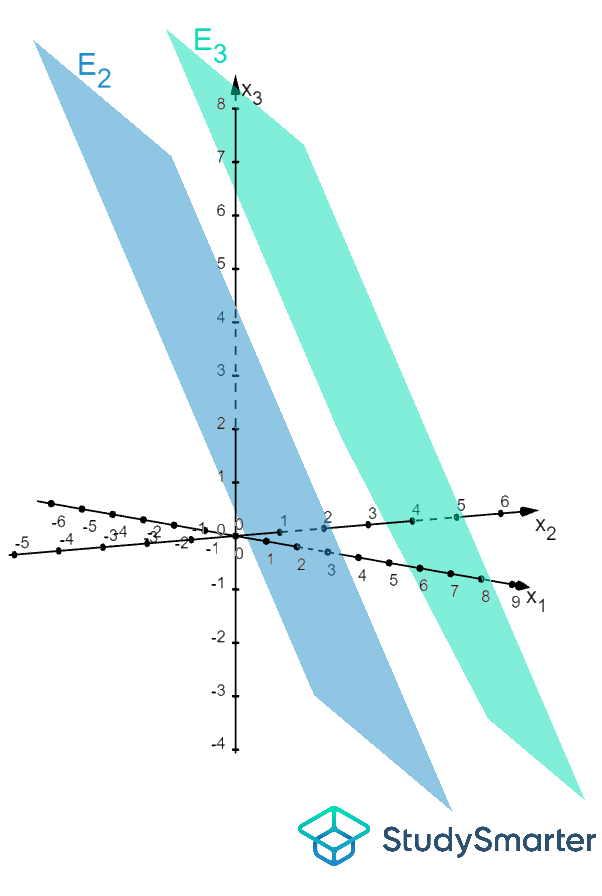
Abstand paralleler Ebenen Lage Koordinatensystem StudySmarter

Abbildung 2: Lage der Ebenen E₂ und E₃ in einem Koordinatensystem

Du kannst also mithilfe der Normalenvektoren überprüfen, ob zwei Ebenen parallel sind.

Aber wieso jetzt eigentlich das Ganze?

Nur wenn zwei Ebenen parallel sind, ergibt es überhaupt Sinn, den Abstand der Ebenen zu berechnen.

Stell Dir vor Deine Zimmerdecke ist nicht parallel zu deinem Zimmerboden, zum Beispiel, weil Du eine Dachschräge hast. An welcher Stelle misst Du dann überhaupt den Abstand? Er wäre ja überall unterschiedlich. Du könntest dann nicht sagen: "Mein Zimmer ist 2,20 m hoch". Denn es ist ja überall unterschiedlich hoch.

Deswegen wird ein Abstand zwischen Ebenen nur dann berechnet, wenn die Ebenen parallel sind. Bevor Du also den Abstand zweier Ebenen berechnest, solltest Du die Lagebeziehung der Ebenen überprüfen.

Abstand paralleler Ebenen – Abstand zweier paralleler Ebenen berechnen

Benötigt wird jetzt ein Rechenweg, mit dem der Abstand zwischen zwei parallelen Ebenen berechnet werden kann.

In deinem Zimmer langt es dafür aus, von einem Punkt auf dem Boden senkrecht nach oben zu messen. Ähnlich ist es in der Mathematik.

Für zwei parallele Ebenen $E_{1}, E_{2}$ hat jeder Punkt $P$ der einen Ebenen den gleichen Abstand zur anderen Ebene.

Der Abstand eines Punktes zur anderen Ebene ist gleichzeitig der Abstand der beiden Ebenen.

Wichtig dabei zu verstehen ist, dass Du nicht zwei beliebige Punkte in den Ebenen wählen kannst und dann deren Abstand bestimmst. Das wäre so, als wenn du in deinem Zimmer nicht senkrecht nach oben misst, sondern quer zu irgendeinem anderen Punkt an der Decke.

Deswegen kannst du dir das "Messen" mathematisch so wie in Abbildung 2 vorstellen: Du wählst einen beliebigen Punkt $P_{1}$ in einer der Ebenen. Von diesem Punkt musst Du nun aber genau senkrecht zur anderen Ebene "messen". Da Du nicht einfach mit einem Geodreieck nachmessen kannst, muss dieser Abstand berechnet werden.

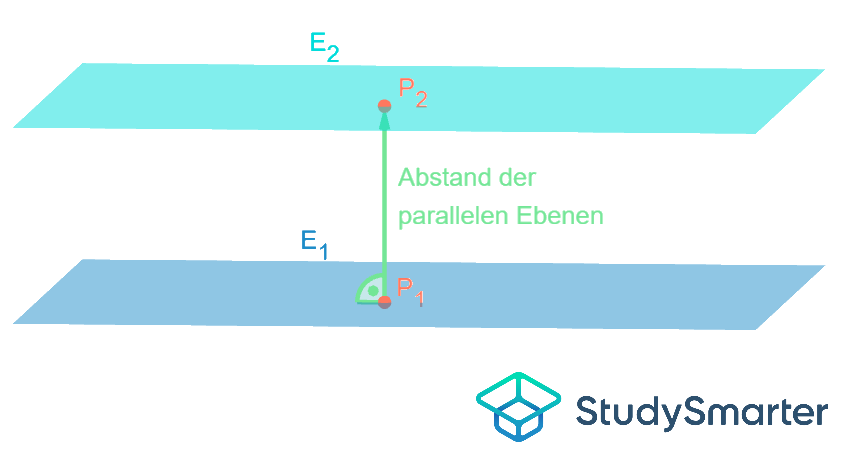
Abstand paralleler Ebenen Abstand Punkte StudySmarter

Abbildung 4: Abstand paralleler Ebenen als Abstand zwischen zwei Punkten

Es gibt zwei unterschiedliche Möglichkeiten diesen Abstand zu berechnen: mit der Hesseschen Normalform oder mit einer Hilfsgeraden

Abstand von Ebene zu Ebene mit der Hesseschen Normalform

Die Hessesche Normalform ist eine Sonderform der Ebenengleichungen. Der Normalenvektor wird normiert, das bedeutet, dass seine Länge 1 ist.

Du kannst die Hessesche Normalform analog zur Koordinatenform angegeben.

Die Hessesche Normalform (HNF) einer Ebene $E$ ist

$H N F E : \frac{a \cdot x_{1} + b \cdot x_{2} + c \cdot x_{3} + d}{|\vec{n}|} = 0$

Dabei ist $a \cdot x_{1} + b \cdot x_{2} + c \cdot x_{3} + d = 0$ die Koordinatenform der Ebenengleichung. $|\vec{n}|$ ist die Länge des Normalenvektors.

Du stellst die Hessesche Normalform also auf, indem du die Koordinatengleichung einer Ebene $E$ durch die Länge des Normalenvektors $\vec{n}$ der Ebene teilst. In diese Hessesche Normalform kannst Du jetzt einen beliebigen Punkt der anderen Ebene einsetzen und erhältst als Ergebnis den Abstand der Ebenen. Beachte dabei aber, dass der Abstand stets positiv ist und deswegen der Zähler Betragsstriche bekommt.

Gegeben sind die Ebene $E_{2}$ und $E_{3}$ wie eben. $E_{2} : 2 \cdot x_{1} + 4 \cdot x_{2} + 2 \cdot x_{3} = 4$ , $E_{3} : [\begin{matrix} \vec{x} - (\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) \end{matrix}] \circ (\begin{matrix} 1 \\ 2 \\ 1 \end{matrix}) = 0$ .

Eine Ebene liegt bereits in Koordinatenform vor, die andere in Normalform. $E_{2}$ ist in Koordinatenform, deswegen wird sie für die Hessesche Normalform verwendet.

Der Normalenvektor der Ebene $E_{2}$ ist $\vec{n} = (\begin{matrix} 2 \\ 4 \\ 2 \end{matrix})$ . Die Länge des Normalenvektors ist $|\vec{n}| = \sqrt{2^{2} + 4^{2} + 2^{2}} = \sqrt{24}$ .

Jetzt stellst Du die Ebenengleichung so um, dass rechts die 0 steht.

$\begin{matrix} 2 \cdot x_{1} + 4 \cdot x_{2} + 2 \cdot x_{3} = 4 & | - 4 \\ 2 \cdot x_{1} + 4 \cdot x_{2} + 2 \cdot x_{3} - 4 = 0 \end{matrix}$

Diese Ebenengleichung teilst Du nun durch die Länge des Normalenvektors und erhältst die Hessesche Normalform (HNF):

$H N F E_{2} : \frac{2 \cdot x_{1} + 4 \cdot x_{2} + 2 \cdot x_{3} - 4}{\sqrt{24}} = 0$

Jetzt wählst du einen beliebigen Punkt aus $E_{3}$ aus. Dazu eignet sich gut der Punkt $P$ aus der Normalenform, $P = (1 / 3 / 1)$ .

Diesen setzt du in die Hessesche Normalenform ein und das Ergebnis ist der Abstand der Ebenen.

$d = \frac{|2 \cdot 1 + 4 \cdot 3 + 2 \cdot 1 - 4|}{\sqrt{24}} = \frac{12}{\sqrt{24}} \approx 2, 45$

Die Ebene $E_{1}$ und $E_{2}$ haben also einen Abstand von 2,45 Längeneinheiten.

Abstand paralleler Ebenen berechnen mit Formel aus Koordinatenform

Zusammengefasst berechnest Du den Abstand zweier paralleler Ebenen mit der Hesseschen Normalform so:

Länge des Normalenvektors $\vec{n}$ der ersten Ebene berechnen.
Hessesche Normalenform dieser Ebene aufstellen, indem du die Koordinatenform nach 0 auflöst und durch die Länge des Normalenvektors teilst
Punkt $P (x_{1} | x_{2} | x_{3})$ aus der zweiten Ebene bestimmen.
Diesen Punkt in die Hessesche Normalenform einsetzen:

d = \frac{|a \cdot x_{1} + b \cdot x_{2} + c \cdot x_{3} + d|}{|\vec{n}|}

Hessesche Normalform aus Normalenform

Eigentlich ist die Hessesche Normalform, wie es der Name schon vermuten lässt, eine Sonderform der Normalenform. Du kannst sie deswegen auch mithilfe der Normalenform aufstellen. Auch hier teilst Du die Normalform durch die Länge des Normalenvektors und es ist:

$H N F E : [\vec{x} - \vec{p}] \circ \frac{\vec{n}}{|\begin{matrix} \vec{n} \end{matrix}|} = 0$

Lass Dich also nicht verwirren, wenn du die eine oder die andere Darstellung aus der Schule kennst. Du kannst die Hessesche Normalform sowohl aus der Koordinatenform als auch aus der Normalform aufstellen. Beide Möglichkeiten sind richtig. Welche Du wählst kann auch davon abhängen, in welcher Form die Ebenengleichung gegeben ist.

Wenn die Ebene in Normalform gegeben ist, bietet es sich an, auch mit dieser die Hessesche Normalform aufzustellen.

Gegeben ist wieder die Ebene $E_{3} : [\begin{matrix} \vec{x} - (\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) \end{matrix}] \circ (\begin{matrix} 1 \\ 2 \\ 1 \end{matrix}) = 0$ . Diese ist in Normalform.

Auch hier berechnest Du jetzt die Länge des Normalenvektors, der in der Normalform mit angegeben ist.

$|\vec{n}| = \sqrt{1^{2} + 2^{2} + 1^{2}} = \sqrt{6}$

Jetzt kannst Du die Normalform durch die Länge des Normalenvektors teilen und erhältst die Hessesche Normalenform.

$H N F E_{3} : [\begin{matrix} \vec{x} - (\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) \end{matrix}] \circ (\begin{matrix} 1 \\ 2 \\ 1 \end{matrix}) \cdot \frac{1}{\sqrt{6}} = 0$

Auch hier setzt Du einen Punkt aus der anderen Ebene ein uns berechnest so den Abstand der Ebenen.

Punkt aus Ebenengleichung bestimmen

Um den Abstand zweier paralleler Ebene mit der Hesseschen Normalenform zu berechnen, setzt Du einen Punkt aus der zweiten Ebene ein. Wenn diese Ebene in Normalform oder Parameterform angegeben ist, kannst Du den Punkt aus der Ebenengleichung ablesen. Ist die Ebene aber in Koordinatenform gegeben, bestimmst Du zuerst einen Punkt, der in der Ebene liegt.

Im letzten Beispiel wurde die Hessesche Normalform der Ebene $E_{3}$ berechnet. Dort setzt Du jetzt einen Punkt aus der Ebene $E_{2}$ ein. Diese ist aber in Koordinatenform angegeben: $E_{2} = 2 \cdot x_{1} + 4 \cdot x_{2} + 2 \cdot x_{3} = 4$

Du bestimmst jetzt $x_{1}, x_{2}, x_{3}$ so, dass die Gleichung richtig ist. Du kannst dich Fragen: "Welche Werte kann ich in die Gleichung einsetzen, sodass das Ergebnis 4 ist?" Hier gibt es unendlich viele Möglichkeiten.

Du kannst zum Beispiel festlegen, dass $x_{1} = 0$ und $x_{3} = 0$ ist. Dann bestimmst du $x_{2}$ .

$\begin{matrix} 2 \cdot 0 + 4 \cdot x_{2} + 2 \cdot x_{3} = 4 \\ 4 \cdot x_{2} = 4 \\ \begin{array}{rcl} x_{2} & = & 1 \end{array} \end{matrix}$

Der Punkt $P = (0 / 1 / 0)$ liegt also in der Ebene $E_{2}$ .

Diesen Punkt kannst Du jetzt in die Hessesche Normalenform aus dem vorherigen Beispiel einsetzen und den Abstand der Ebenen ausrechnen. Achte auch hier auf die Betragsstriche:

$\begin{array}{rc} d = & |[\begin{matrix} (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}) - (\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) \end{matrix}] \circ (\begin{matrix} 1 \\ 2 \\ 1 \end{matrix})| \cdot \frac{1}{\sqrt{6}} \\ = & |(\begin{matrix} - 1 \\ - 2 \\ - 1 \end{matrix}) \circ (\begin{matrix} 1 \\ 2 \\ 1 \end{matrix})| \cdot \frac{1}{\sqrt{6}} \\ = & |(- 1) \cdot 1 + (- 2) \cdot 2 + (- 1) \cdot 1| \cdot \frac{1}{\sqrt{6}} \\ = & |- 1 - 4 - 1| \cdot \frac{1}{\sqrt{6}} \\ = & \frac{|- 6|}{\sqrt{6}} = \frac{6}{\sqrt{6}} \approx 2, 45 \end{array}$

Wenn du einen Punkt mithilfe der Koordinatenform bestimmen willst, mach es dir besonders einfach und wähle zwei Koordinaten gleich 0. Dann musst du nur die Dritte bestimmen.

Abstand Ebene zu Ebene berechnen mit einer Hilfsgeraden mit Lotfußpunkt

Es gibt noch eine zweite Möglichkeit, um den Abstand von parallelen Ebenen zu bestimmen. Diese verwendet nicht die Hessesche Normalform, sondern eine Hilfsgerade mit Lotfußpunkt.

Gegeben sind zwei parallele Ebenen $E_{1}, E_{2}$ . Um den Abstand dieser Ebenen zu berechnen, stellst Du eine Hilfsgerade auf, die senkrecht zu den Ebenen steht. Dazu verwendest du den Normalenvektor $\vec{n_{1}}$ der Ebene $E_{1}$ . Aus der anderen Ebene $E_{2}$ wählst du einen Punkt $P_{2}$ und verwendest diesen als Stützpunkt der Hilfsgeraden. Die Gerade verläuft dann also senkrecht zur Ebene und durch diesen Punkt. Deswegen wird dieser Punkt auch Lotfußpunkt genannt. Die Gerade durch den Punkt $P_{2}$ kannst du in Abbildung 3 finden.

Die Geradengleichung der Hilfsgeraden ist:

$g : \vec{x} = \vec{p_{2}} + r \cdot \vec{n_{1}}$

Abstand paralleler Ebenen Hilfsgerade Lotfußpunkt StudySmarter Abbildung 5: Hilfsgerade g durch den Punkt P₂ senkrecht zu den parallelen Ebenen

Wenn Du die Hilfsgerade aufgestellt hast, berechnest Du als nächstes den Schnittpunkt dieser Hilfsgeraden mit der Ebene $E_{1}$ (also mit der Ebene, die nicht den Stützpunkt der Geraden enthält).

Gesucht ist jetzt also der Schnittpunkt einer Geraden mit einer Ebene. Dazu berechnest Du zuerst die Koordinaten eines beliebigen Punktes auf der Hilfsgeraden, indem du die einzelnen Zeilen der Geradengleichung ausrechnest.

$g : \vec{x} = (\begin{matrix} p_{2_{1}} \\ p_{2_{2}} \\ p_{2_{3}} \end{matrix}) + r \cdot (\begin{matrix} n_{1_{1}} \\ n_{1_{2}} \\ n_{1_{3}} \end{matrix})$

Dann ist $x_{1} = {p_{2}}_{1} + r \cdot {n_{1}}_{1}$ , $x_{2} = {p_{2}}_{2} + r \cdot {n_{1}}_{2}$ , $x_{3} = p_{2_{3}} + r \cdot n_{1_{3}}$ . Lass dich nicht von den viele Indizes verwirren. Das sieht nur so aus, da die Vektoren selber schon Indizes hatten. Aus der Schule kennst du es vielleicht mit anderen Beschriftungen.

Diese Werte für $x_{1}, x_{2}, x_{3}$ setzt Du nun in die Ebenengleichung der Ebene $E_{1}$ ein. Am einfachsten ist dies, wenn Du die Ebenengleichung in Koordinatenform hast. Dann erhältst du die Gleichung:

$a \cdot ({p_{2}}_{1} + r \cdot {n_{1}}_{1}) + b \cdot ({p_{2}}_{2} + r \cdot {n_{1}}_{2}) + c \cdot ({p_{2}}_{3} + r \cdot {n_{1}}_{3}) + d = 0$

Die Gleichung vereinfachst Du und löst nach $r$ auf. Dann setzt Du den Wert für $r$ in die Geradengleichung ein und berechnest den Schnittpunkt $S$ .

Jetzt kennst Du den Schnittpunkt $S$ der Hilfsgeraden $g$ mit der Ebene $E_{1}$ und den Lotfußpunkt $P_{2}$ der Geraden $g$ in $E_{2}$ .

Als letzten Schritt berechnest Du den Abstand der Punkte $S$ und $P_{2}$ . Der Abstand dieser Punkte entspricht genau dem Abstand der beiden Ebenen.

$d_{E_{1}, E_{2}} = d_{S, P_{2}} = |\vec{S P}|$

Gegeben sind die Ebenen $E_{2}, E_{3}$ wie in den Beispiel zuvor: $E_{2} : 2 \cdot x_{1} + 4 \cdot x_{2} + 2 \cdot x_{3} = 4$ , $E_{3} : [\begin{matrix} \vec{x} - (\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) \end{matrix}] \circ (\begin{matrix} 1 \\ 2 \\ 1 \end{matrix}) = 0$ $E_{2}$ ist bereits in Koordinatenform. Deswegen kannst Du sie gut verwenden, um später die Punkte der Gerade einzusetzen. Das bedeutet, Du benötigst für deine Hilfsgerade $g$ den Normalenvektor $\vec{n_{2}}$ von $E_{2}$ und einen Punkt aus $E_{3}$ .

Den Normalenvektor kannst du aus der Ebengleichung anhand der Faktoren ablesen: $\vec{n_{2}} = (\begin{matrix} 2 \\ 4 \\ 2 \end{matrix})$ . Bestimme nun einen Punkt in der Ebene 3. Hier kannst Du den Punkt $P_{3} = (1 | 3 | 1)$ aus der Geradengleichung verwenden. $P_{3}$ ist nun der Lotfußpunkt der Geraden $g$ und $\vec{n_{2}}$ der Richtungsvektor. Es ist:

$g : \vec{x} = (\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) + r \cdot (\begin{matrix} 2 \\ 4 \\ 2 \end{matrix})$

Gesucht ist nun der Schnittpunkt dieser Geraden $g$ mit der Ebene $E_{2}$ . Dazu berechnest Du zuerst die Koordinaten eines beliebigen Punktes auf der Geraden $g$ . Diese sind $x_{1} = 1 + 2 r, x_{2} = 3 + 4 r, x_{3} = 1 + 2 r$ .

Diese Koordinaten setzt Du in die Ebenengleichung von $E_{2}$ ein.

$2 \cdot (1 + 2 r) + 4 \cdot (3 + 4 r) + 2 \cdot (1 + 2 r) = 4$

Löse die Gleichung nun nach $r$ auf.

$\begin{matrix} 2 \cdot (1 + 2 r) + 4 \cdot (3 + 4 r) + 2 \cdot (1 + 2 r) = 4 \\ \Leftrightarrow & 2 + 4 r + 12 + 16 r + 2 + 4 r = 4 \\ \Leftrightarrow & 16 + 24 r = 4 & | - 16 \\ \Leftrightarrow & 24 r = - 12 & | : 24 \\ \Leftrightarrow & r = - \frac{1}{2} \end{matrix}$

Setze $r = - \frac{1}{2}$ in die Geradengleichung ein und berechne den Schnittpunkt $S$ .

$\vec{S} = (\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) - \frac{1}{2} \cdot (\begin{matrix} 2 \\ 4 \\ 2 \end{matrix}) = (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix})$

Als letzten Schritt bestimmst Du nun den Abstand der Punkte $S$ und $P_{3}$ . Der Abstand der Punkt entspricht genau der Länge des Verbindungsvektors.

$d_{S, P_{3}} = |\vec{S P_{3}}| = |(\begin{matrix} 1 \\ 3 \\ 1 \end{matrix}) - (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix})| = |(\begin{matrix} 1 \\ 2 \\ 1 \end{matrix})| = \sqrt{1^{2} + 2^{2} + 1^{2}} = \sqrt{6} \approx 2, 45$

Der Abstand der Punkte $S$ und $P_{3}$ beträgt 2,45 Längeneinheiten. Dies ist auch der Abstand der beiden Ebenen.

Zusammengefasst kannst Du so vorgehen, um den Abstand zweier paralleler Geraden mit einer Hilfsgeraden mit Lotfußpunkt zu bestimmen:

Hilfsgerade $g$ senkrecht zur Ebene (Normalenvektor als Richtungsvektor) und durch Lotfußpunkt $P$ in $E_{2}$ aufstellen
Schnittpunkt $S$ der Geraden mit der Ebene $E_{1}$ berechnen
Abstand der Punkte $P, S$ bestimmen

Jetzt kennst Du zwei Möglichkeiten, um den Abstand paralleler Ebenen zu berechnen. Ob Du die Hessesche Normalform oder die Hilfsgerade verwendest, hängt zum einen davon ab, welchen Weg Du lieber magst, zum anderen aber auch davon, ob die Aufgaben einen Weg vorgibt. Wenn kein Weg vorgegeben ist, kannst Du das wählen, was Dir leichter erscheint.

Abstand paralleler Ebenen – Aufgaben mit Lösungen

Mit diesen Aufgaben kannst Du üben, den Abstand zwischen parallelen Ebenen zu berechnen.

Aufgabe 1

Gegeben sind die beiden parallelen Ebenen $E_{1} : x_{1} + 2 x_{2} - 3 x_{3} = 4$ und $E_{2} : [\vec{x} - (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix})] \circ (\begin{matrix} 2 \\ 4 \\ - 6 \end{matrix}) = 0$ .

a) Bestimme die Hessesche Normalform der Ebene $E_{1}$ .

b) Berechne den Abstand der beiden Ebenen.

Lösung

Ein Normalenvektor $\vec{n_{1}}$ der Ebene $E_{1}$ ist $\vec{n_{1}} = (\begin{matrix} 1 \\ 2 \\ - 3 \end{matrix})$ . Diesen kannst Du aus den Faktoren vor den x in der Ebenengleichung ablesen. Die Länge des Normalenvektors ist:

$|\vec{n}| = \sqrt{1^{2} + 2^{2} + {(- 3)}^{2}} = \sqrt{14}$

Die Koordinatengleichung der Ebene stellst Du jetzt so um, dass rechts vom Gleichheitszeichen die 0 steht.

$\begin{matrix} x_{1} + 2 x_{2} - 3 x_{3} = 4 & | - 4 \\ \Leftrightarrow & x_{1} + 2 x_{2} - 3 x_{3} - 4 = 0 \end{matrix}$

Die Hessesche Normalform der Ebene $E_{1}$ ist:

$E_{1} : \frac{x_{1} + 2 x_{2} - 3 x_{3} - 4}{\sqrt{14}} = 0$

In der Aufgabenstellung steht bereits, dass die Ebenen parallel sind. Dies brauchst du also nicht mehr zu überprüfen.

Da in a) bereits die Hessesche Normalform berechnet wurde, ist es auf jeden Fall sinnvoll, den Abstand der Ebenen mithilfe der Hesseschen Normalform zu bestimmen und nicht mit einer Hilfsgeraden.

In die Hessesche Normalform setzt du nun einen Punkt der Ebene $E_{2}$ ein. Dazu kannst du gut den Punkt $P_{2}$ aus der Ebenengleichung nehmen: $P_{2} = (0 | 1 | 0)$

$d_{E_{1}, E_{2}} = \frac{|0 + 2 \cdot 1 - 3 \cdot 0 - 4|}{\sqrt{14}} = \frac{|2 - 4|}{\sqrt{14}} = \frac{|- 2|}{\sqrt{14}} = \frac{2}{\sqrt{14}} \approx 0, 53$

Der Abstand der Ebenen $E_{1}$ und $E_{2}$ beträgt 0,53 Längeneinheiten.

Aufgabe 2

Gegeben sind die parallelen Ebenen $E_{1} : 2 x_{1} - 6 x_{2} - 4 x_{3} + 2 = 0$ und $E_{2} : x_{1} - 3 x_{2} - 2 x_{3} + 2 = 0$ .

Berechne den Abstand der Ebenen mit einer Hilfsgeraden mit Lotfußpunkt.

Lösung

Als Erstes stellst Du die Hilfsgerade auf. Du kannst selbst entscheiden, ob ihr Lotfußpunkt in $E_{1}$ oder in $E_{2}$ liegen soll. Hier wird der Lotfußpunkt jetzt in $E_{2}$ gewählt. Du benötigst also einen Punkt, der in $E_{2}$ liegt.

Wähle dazu zum Beispiel $x_{1} = x_{2} = 0$ und $x_{3} = 1$ . Dann hast Du den Punkt $P_{2} = (0 | 0 | 1)$ , der die Ebenengleichung von $E_{2}$ erfüllt.

Ein Normalenvektor der Ebene $E_{1}$ ist $\vec{n_{1}} = (\begin{matrix} 2 \\ - 6 \\ - 4 \end{matrix})$ . Jetzt kannst Du eine Hilfsgerade $g$ aufstellen.

$g : \vec{x} = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}) + r \cdot (\begin{matrix} 2 \\ - 6 \\ - 4 \end{matrix})$

Im nächsten Schritt berechnest Du den Schnittpunkt der Geraden $g$ mit der Ebene $E_{1}$ .

Für einen beliebigen Punkt auf $g$ ist $x_{1} = 2 r, x_{2} = - 6 r, x_{3} = 1 - 4 r$ . Diese Werte setzt Du in die Ebenengleichung von $E_{1}$ ein und löst nach $r$ auf, um den Schnittpunkt zu ermitteln.

$\begin{matrix} 2 \cdot 2 r - 6 \cdot (- 6 r) - 4 \cdot (1 - 4 r) + 2 = 0 \\ \Leftrightarrow & 4 r + 36 r - 4 + 16 r + 2 = 0 \\ \Leftrightarrow & 56 r - 2 = 0 & | + 2 \\ \Leftrightarrow & 56 r = 2 & | : 56 \\ \Leftrightarrow & r = \frac{1}{28} \end{matrix}$

Diesen Wert für $r$ setzt Du in die Geradengleichung ein und erhältst den Schnittpunkt $S$ .

$\vec{S} = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}) + \frac{1}{28} \cdot (\begin{matrix} 2 \\ - 6 \\ - 4 \end{matrix}) = (\begin{matrix} 0 + \frac{1}{28} \cdot 2 \\ 0 + \frac{1}{28} \cdot (- 6) \\ 1 + \frac{1}{28} \cdot (- 4) \end{matrix}) = (\begin{matrix} \frac{1}{14} \\ \frac{- 3}{14} \\ \frac{6}{7} \end{matrix})$

Als Letztes berechnest du den Abstand zwischen dem Lotfußpunkt $P_{2}$ und dem Punkt $S$ .

$d_{P_{2}, S} = |\vec{P_{2} S}| = |(\begin{matrix} \frac{1}{14} \\ \frac{- 3}{14} \\ \frac{6}{7} \end{matrix}) - [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}]| = |(\begin{matrix} \frac{1}{14} \\ \frac{- 3}{14} \\ \frac{- 1}{7} \end{matrix})| = \sqrt{{(\frac{1}{14})}^{2} + {(\frac{- 3}{14})}^{2} + {(\frac{- 1}{7})}^{2}} = \sqrt{\frac{1}{14}} \approx 0, 27$

Der Abstand der beiden Ebenen $E_{1}$ und $E_{2}$ beträgst 0,27 Längeneinheiten.

Abstand paralleler Ebenen – Das Wichtigste

Der Abstand paralleler Ebenen wird berechnet, indem du dem Abstand von einem beliebigen Punkt der einen Ebene zur andere Ebene bestimmst.
Du kannst den Abstand paralleler Ebenen mithilfe der Hesseschen Normalenform berechnen:
- Stelle die Hessesche Normalform einer der beiden Ebenen auf.
- Setze einen Punkt der anderen Eben in diese Normalform ein.
- Es ist $d = \frac{|a \cdot x_{1} + b \cdot x_{2} + c \cdot x_{3} + d|}{|\vec{n}|}$ .
Du kannst den Abstand aber auch mit einer Hilfsgeraden mit Lotfußpunkt bestimmen:
- Stelle die Hilfsgerade senkrecht zu den Eben auf. Der Stützvektor (Lotfußpunkt) der Gerade ist ein Punkt der einen Ebene. Der Richungsvektor ist ein Normalenvektor der anderen Ebene.
- Berechne den Schnittpunkt der Geraden mit der Ebene, in der nicht der Lotfußpunkt liegt.
- Bestimme den Abstand des Schnittpunktes und des Lotfußpunktes.

Karteikarten in Abstand paralleler Ebenen 2

Lerne jetzt

Welche Aussage über den Abstand paralleler Ebenen ist richtig?

Alle Punkte der einen Ebene haben immer denselben Abstand zur anderen Ebene.

Wie wird der Abstand zwischen parallelen Ebenen berechnet?

Wähle die richtige Aussage aus.

Es wird der Abstand eines beliebigen Punktes der einen Ebene zur anderen Ebene berechnet.

Mit E-Mail registrieren

Du hast bereits ein Konto? Anmelden

Häufig gestellte Fragen zum Thema Abstand paralleler Ebenen

Wie berechne ich den Abstand paralleler Ebenen?

Den Abstand paralleler Ebenen kannst Du mit der Hesseschen Normalform oder mit einer Hilfsgeraden mit Lotfußpunkt bestimmen. In beiden Fällen berechnest Du dann den Abstand von einem Punkt zur Ebene.

Wann sind zwei Ebenen parallel?

Zwei Ebenen sind parallel, wenn sie an jeder Stelle denselben Abstand zueinander haben. Sie schneiden sich nicht.

Mathematisch kannst Du parallele Ebenen daran erkennen, dass ihre Normalenvektoren linear abhängig sind.

Wie berechnet man ob zwei Ebenen parallel sind?

Um zu berechnen, ob zwei Ebenen parallel sind, kannst du ihre Normalenvektoren betrachten. Wenn diese linear Abhängig voneinander sind, sind die Ebenen entweder parallel oder identisch. Um zu bestimmen, ob sie echt parallel sind, kannst du überprüfen, ob ein beliebiger Punkt der einen Ebene in der anderen Ebene liegt. Ist dies nicht der Fall, sind die Ebenen parallel.

Wie stelle ich parallele Ebenen auf?

Parallele Ebenen kannst du am besten mithilfe der Normalenvektoren aufstellen. Verwende linear abhängige Normalenvektoren. Dann sind die Ebenen parallel.

Erklärung speichern

Entdecke Lernmaterialien mit der kostenlosen StudySmarter App

Kostenlos anmelden

Über StudySmarter

StudySmarter ist ein weltweit anerkanntes Bildungstechnologie-Unternehmen, das eine ganzheitliche Lernplattform für Schüler und Studenten aller Altersstufen und Bildungsniveaus bietet. Unsere Plattform unterstützt das Lernen in einer breiten Palette von Fächern, einschließlich MINT, Sozialwissenschaften und Sprachen, und hilft den Schülern auch, weltweit verschiedene Tests und Prüfungen wie GCSE, A Level, SAT, ACT, Abitur und mehr erfolgreich zu meistern. Wir bieten eine umfangreiche Bibliothek von Lernmaterialien, einschließlich interaktiver Karteikarten, umfassender Lehrbuchlösungen und detaillierter Erklärungen. Die fortschrittliche Technologie und Werkzeuge, die wir zur Verfügung stellen, helfen Schülern, ihre eigenen Lernmaterialien zu erstellen. Die Inhalte von StudySmarter sind nicht nur von Experten geprüft, sondern werden auch regelmäßig aktualisiert, um Genauigkeit und Relevanz zu gewährleisten.

Erfahre mehr

StudySmarter Redaktionsteam

Team Mathe Lehrer

19 Minuten Lesezeit
Geprüft vom StudySmarter Redaktionsteam

Erklärung speichern

Abstand paralleler Ebenen

StudySmarter Redaktionsteam

Abstand paralleler Ebenen – Ebenengleichungen: Parameterform, Normalenform, Koordinatenform

Abstand paralleler Ebenen – bestimmen

Abstand paralleler Ebenen – Abstand zweier paralleler Ebenen berechnen