In diesem Artikel geht es um den Flächeninhalt eines Trapez. Wir erklären dir, wie die Formel des Flächeninhaltes eines Trapez hergeleitet wird und wie du sie richtig anwendest.
Flächeninhalt Trapez – Berechnung
Bevor wir uns der eigentlichen Flächeninhaltsformel eines Trapez gemeinsam widmen, fassen wir noch einmal kurz zusammen, was eigentlich ein Trapez ausmacht und was unter dem Begriff Flächeninhalt zu verstehen ist.
Ein Trapez zählt zu den speziellen Vierecken, bei dem zwei gegenüberliegende Seiten parallel zueinander sind. Die parallelen Seiten nennt man bei einem Trapez Grundseiten, die zwei anderen Seiten sind die Schenkel. Bei einem Trapez bildet die Summe der an den Schenkeln anliegenden Winkel 180°.
Hinweis: Wenn dir nicht klar ist, was genau ein Trapez ist, solltest du zunächst die Zusammenfassung zum Trapez lesen, bevor du dich mit dieser Zusammenfassung beschäftigst.
Im Folgenden soll der Flächeninhalt eines Trapezes bestimmt werden.
Unter dem Flächeninhalt wird ein Maß einer ebenen, also zweidimensionalen, Figur verstanden. Dieses Maß wird durch die Anzahl der Einheitsquadrate bestimmt, die in der Figur enthalten sind.
Die Formel für die Fläche eines Trapez lautet
Dabei stehen a und c für die Länge der Seiten, die parallel zueinander verlaufen, also die Grundseiten. Die Höhe innerhalb des Trapezes wird mit h bezeichnet.
Abbildung 1: Flächeninhalt eines Trapez und die zugehörigen Größen
Zunächst addierst du die Werte für a und c miteinander und erhältst dann einen Summenwert. Diese Summe multiplizierst du anschließend mit h. Danach dividierst du dein Zwischenergebnis durch 2.
Wieso das so ist, erfährst du im nächsten Abschnitt dieser Zusammenfassung!
Flächeninhalt Trapez – Herleitung Formel
Um sich die Flächeninhaltsformel besser merken zu können, ist es oft hilfreich sich die Herleitung der Formel einmal anzusehen. Dabei gibt es hinsichtlich der Flächeninhaltsformel von Trapezen verschiedene Herleitungsmöglichkeiten: bei der ersten wird ergänzt, bei der zweiten zerlegt. Beide Herleitungen liefern natürlich dieselbe Formel.
Herleitung über die Bildung eines Parallelogramms
| Schritt | Abbildung 2 - 7 Herleitung der Flächeninhaltsformel |
| 1. Wir nehmen unser Trapez ABCD und verdoppeln es einmal. |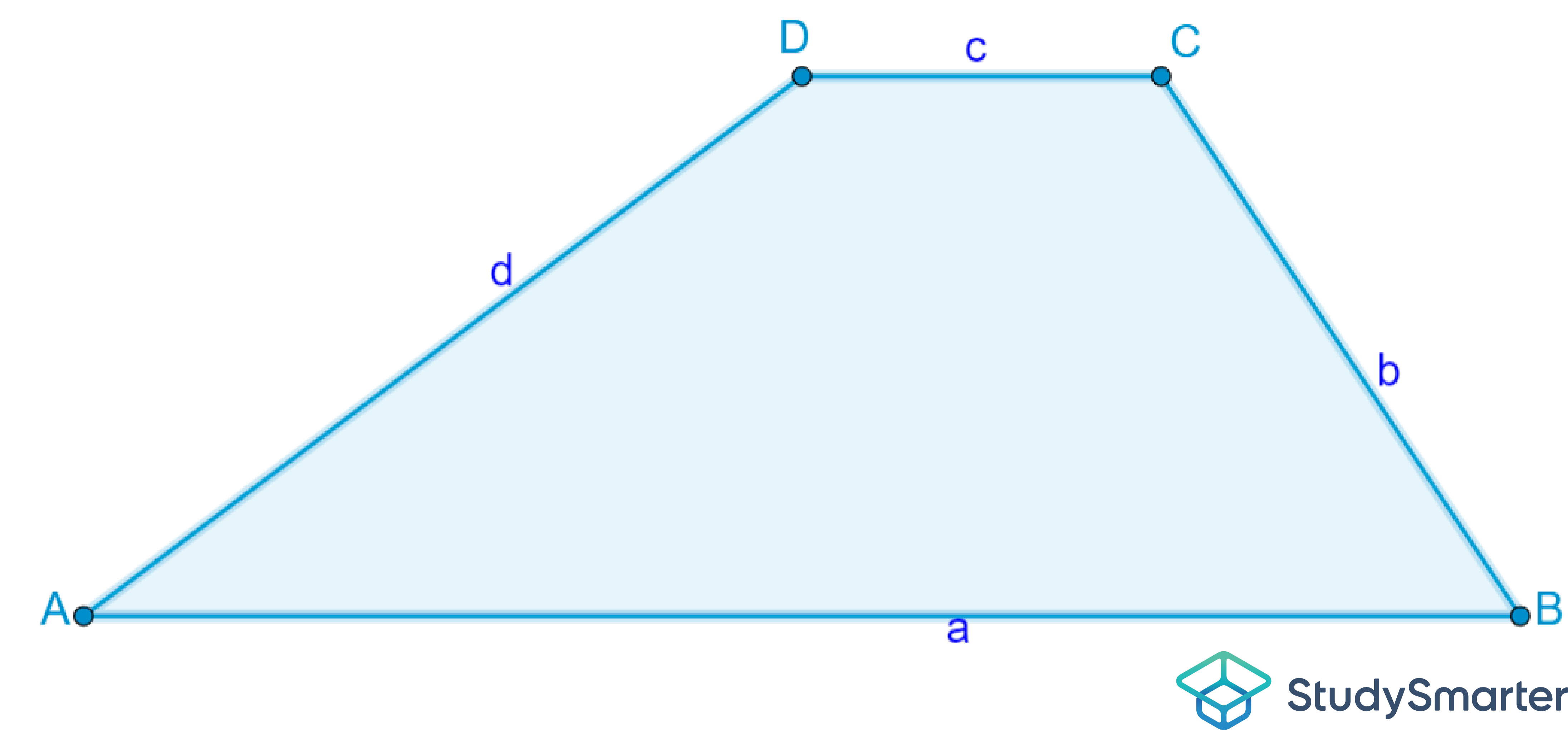 
|
| 2. Nun drehen wir das zweite Trapez um 180° und legen dies passend an das erste Trapez. |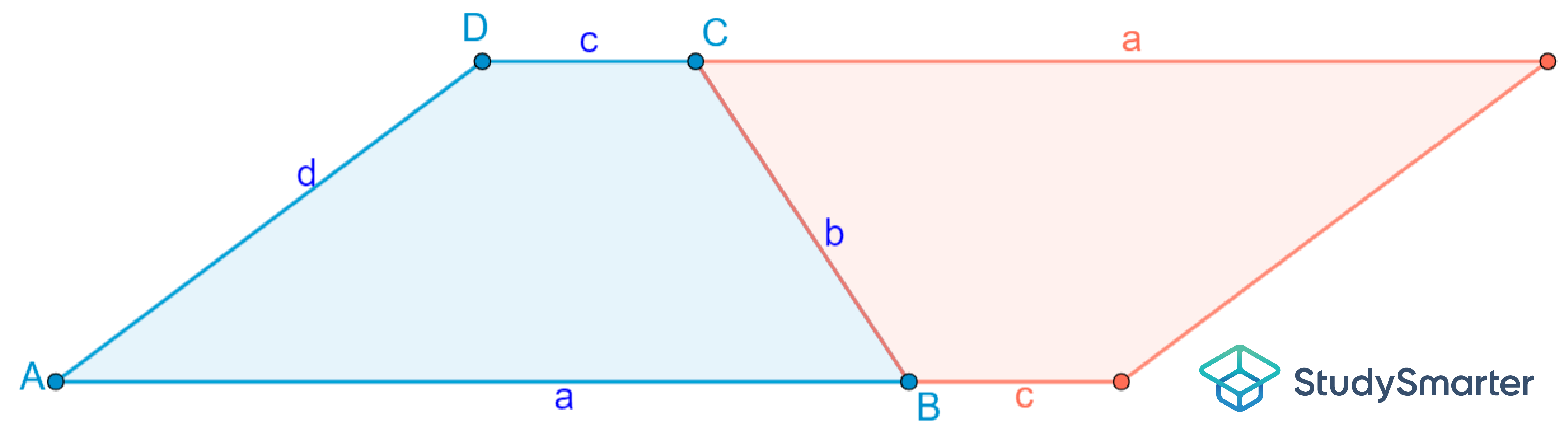 
|
| 3. Durch die Ergänzung des Trapezes haben wir die Fläche eines Parallelogramms ALMD erhalten. |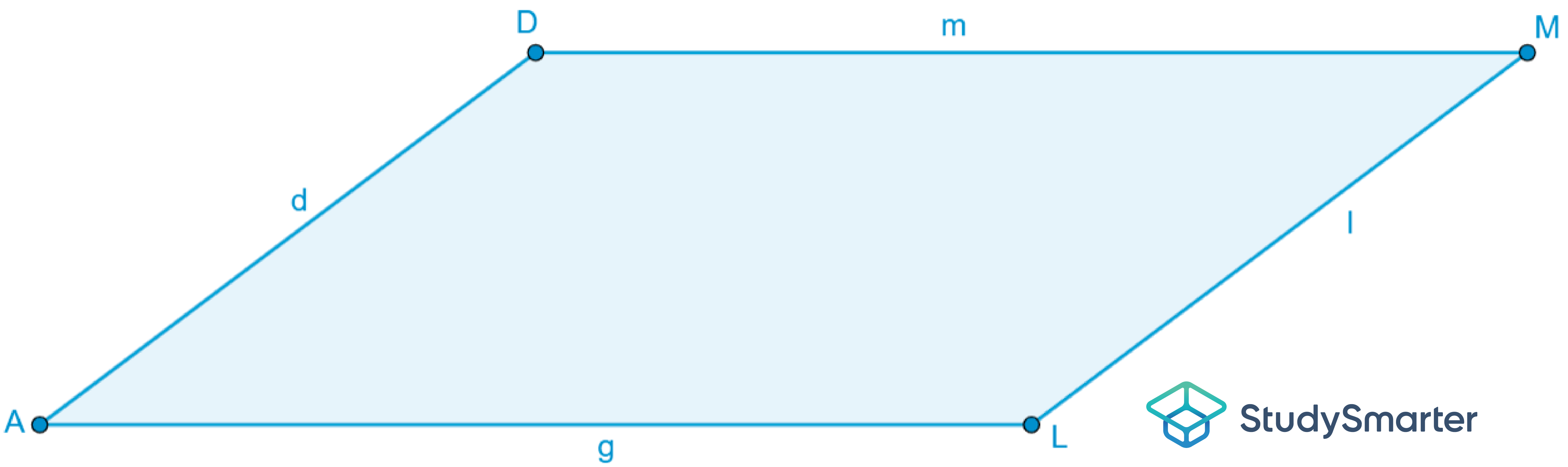 
|
| 4. Die Seite, die senkrecht zur Höhe h steht, wird als Grundseite g bezeichnet. Die Fläche eines Parallelogramms berechnest du grundsätzlich mit folgender Formel: |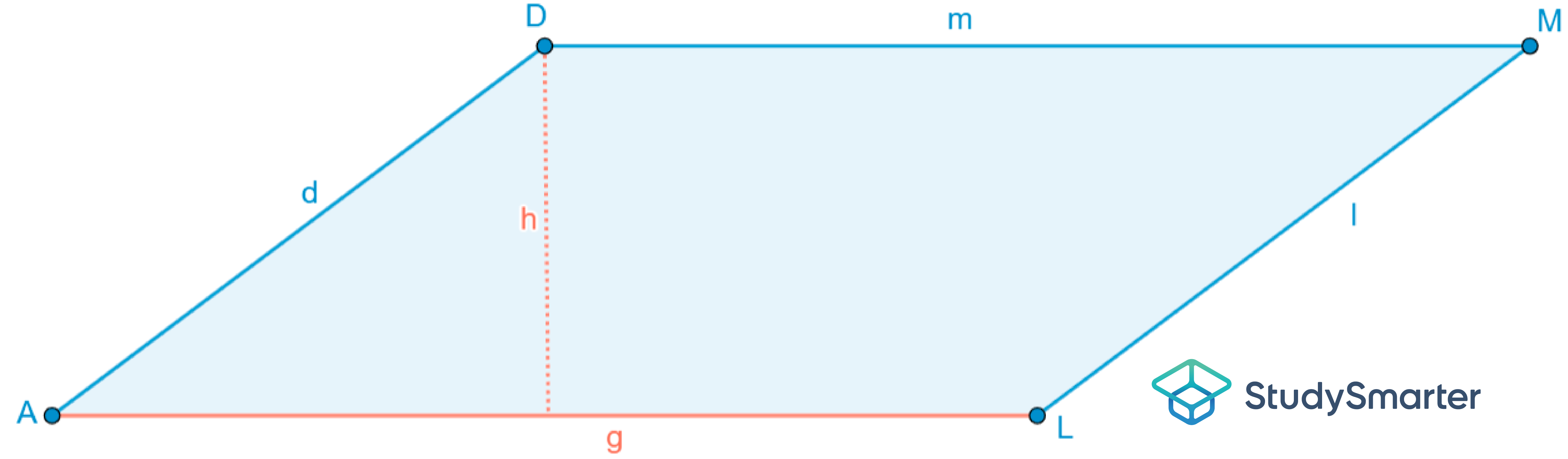 
 |
| 5. Die Seite g des Parallelogramms setzt sich wiederum aus den beiden Seiten a und c zusammen.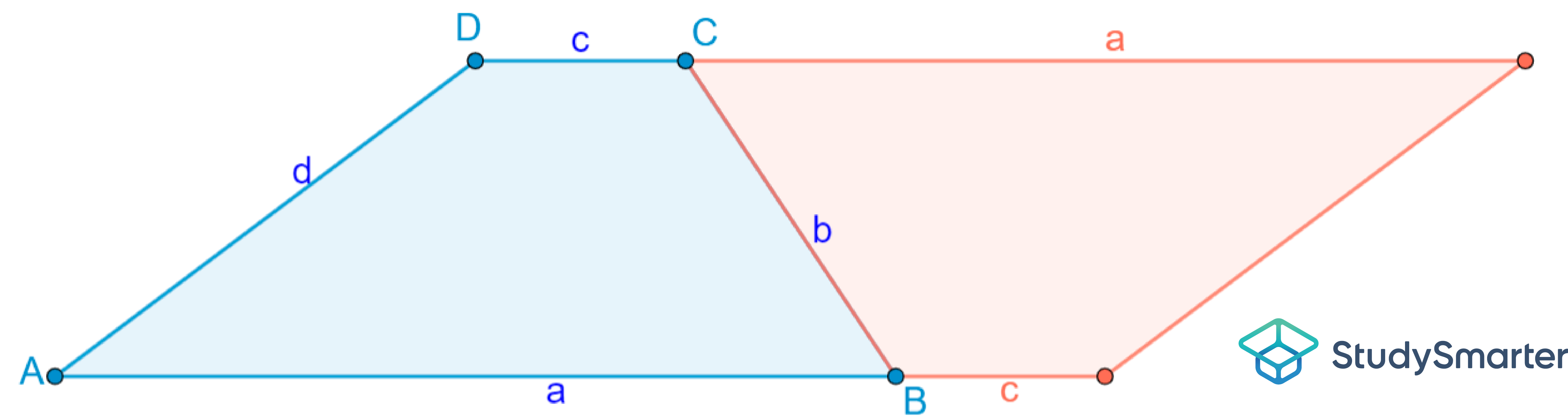 
|
| 6. Nun setzen wir die Summe unserer beiden Seiten in die Flächeninhaltsformel des Parallelogramms ein: |  
|
7. Wir wissen aber, dass unser Parallelogramm aus zwei gleich großen Trapezen bestand und demzufolge die Fläche des Parallelogramms doppelt so groß ist, wie unser eigentliches Trapez.Deswegen multiplizieren wir ganz einfach die Flächeninhaltsformel des Parallelogramms mit  und erhalten unsere Flächeninhaltsformel für das Trapez. |   |
So, jetzt hast du bereits die erste Herleitung der Flächeninhaltsformel eines Trapez kennengelernt. Jetzt geht es mit der zweiten Herleitung weiter.
Herleitung über die Zerlegung in Einzelflächen
Im Gegensatz zur Herleitung durch die Bildung eines Parallelogramms erfolgt die zweite Herleitung über die Zerlegung des Trapez in Einzelflächen. Aber auch hier gehen wir das Schritt für Schritt mit dir durch.
| Schritt | Abbildung 8 - 15 zweite Möglichkeit zur Herleitung der Flächeninhaltsformel |
| 1. Gegeben ist das Trapez ABCD. | 
|
| 2. Wir zerlegen nun unser Trapez ABCD in Einzelflächen. Hier bietet es sich an dies in zwei Dreiecke und ein Rechteck zu teilen.Wir erhalten zwei Dreiecke (d1 und d2) und ein Rechteck (v1).Wie du an den Abbildungen erkennen kannst, ist die Höhe des Trapez genauso groß wie die Höhe der beiden Dreiecke und des Vierecks. | 
|
| 3. Die Fläche unseres Trapez setzt sich somit aus den einzelnen Teilflächen zusammen: |  |
| 4. Jetzt benötigen wir natürlich die Flächeninhaltsformeln für ein Rechteck und die beiden Dreiecke: | 1. Dreieck d1: 
   2. Dreieck:
   Viereck:
  |
| 5. Da wir jetzt alle Formeln für die einzelnen Teilflächen haben, müssen wir sie lediglich addieren, um auf den Flächeninhalt des ursprünglichen Trapez zu kommen. |  | |
| 6. Nun setzen wir die jeweiligen Formeln in die Gesamtgleichung.Wie du anhand der Abbildung erkennen kannst, ist die Seite r so lang wie Differenz der Seitenlängen von a, o und v ist. |  
| 
|
| 7. Anschließend klammern wir zur Vereinfachung h aus. |  | 
|
8. Um die Formel noch übersichtlicher zu gestalten, klammern wir  aus. |  | 
|
| 9. Wie du anhand der Abbildungen erkennen kannst, ist die Seitenlänge von c genauso groß wie Differenz von a, o und v. Somit ersetzen wir c durch c = a-o-v. | | 
|
| 10. Allerdings haben wir zweimal c in der Ausgangsgleichung. Wir ersetzen jedoch nur einmal c = a-o-v, das zweite c erhalten wir in der Gleichung! | 
| |
| 11. Durch die Zusammenfassung der einzelnen Variablen ergibt sich die folgende Formel: |  | |
| 12. Somit erhalten wir unsere Ausgangsformel für den Flächeninhalt eines Trapez. |  | |
Flächeninhalt Trapez – Alternative Formel
Neben der Flächeninhaltsformel, die wir gerade gemeinsam hergeleitet haben, gibt es noch eine zweite, selten genutzte Formel:
Die Berechnung des Flächeninhalts eines Trapez kann ebenso durch die folgende Formel beschrieben werden:
Dabei steht m für die Länge der Mittellinie und berechnet sich wie folgt
Abbildung 16: Flächeninhalt eines Trapez
Du siehst, dass sich jedes Mal die gleiche Formel ergibt, ganz egal, welche Formel du letztendlich verwendest!
Flächeninhalt Trapez – Aufgaben
Aufgabe 1
Deine Eltern möchten in ihrem Garten die Terrasse neu mit Natursteinpflaster verlegen. Dafür gehen sie in den nächstgelegenen Baumarkt und lassen sich vom Fachmann Frank Fliese beraten. Herr Fliese stellt deinen Eltern allerlei Fragen, unter anderem wie groß die Fläche sei, die neu gepflastert werden soll. Deine Eltern bitten dich um Hilfe. Kannst du die Fläche der Terrasse berechnen?
Abbildung 17: Terrassenfläche in Form eines Trapez
Abbildung 17: Terrassenfläche in Form eines Trapez
Dabei haben deine Eltern die folgenden Längen ausgemessen:
a = 5m
c = 3m
h = 2m
Lösung
1. Zur Berechnung der Fläche der Terrasse eignet sich die Formel:
2. Nun musst du lediglich die gegebenen Längen einsetzen:
3. Zum Schluss berechnest du das Ergebnis.
Antwort: die Terrasse hat eine Fläche von 8m².
Aufgabe 2
Du willst mit deinen Freunden eine Mauer im Jugendzentrum bemalen. Die Mauer hat die Form eines rechtwinkligen Trapezes. Von einer vorherigen Aktion, in der die Wand mit Graffiti besprüht wurde, hat ein Betreuer noch die folgenden Abmessungen gefunden:
Abbildung 18: Mauerfläche in Form eines Trapez
Berechne die Länge der Seite d.
Lösung
1. Zuerst stellst du wieder die richtige Formel auf:
2. Nun gilt aber für die Mauer folgendes:
- Die Länge von a entspricht eigentlich der Höhe in der Formel, also a = h.
- Somit ist die Seite d eigentlich die Variable a in der Formel. d = a
- Die zweite parallel verlaufende Seite b entspricht der Variable c in der Flächeninhaltsformel. b = c
3. Somit erhältst du folgende Gleichung:
4. Jetzt setzt du die jeweiligen Werte ein:
Antwort: Die Mauer ist an der Seite d 6,125m hoch.
Flächeninhalt Trapez – Das Wichtigste auf einen Blick
Der Flächeninhalt eines Trapez wird mit Hilfe der folgenden Formel berechnet:
Du kannst die Formel auf verschiedene Art und Weisen herleiten:
Du kannst die Flächeninhaltsformel über die Bildung eines Parallelogramms herleiten.
Die Flächeninhaltsformel kannst du aber auch durch die Zergliederung des Trapez in zwei Dreiecke und ein Viereck nachvollziehen.
Schule 
Studium 
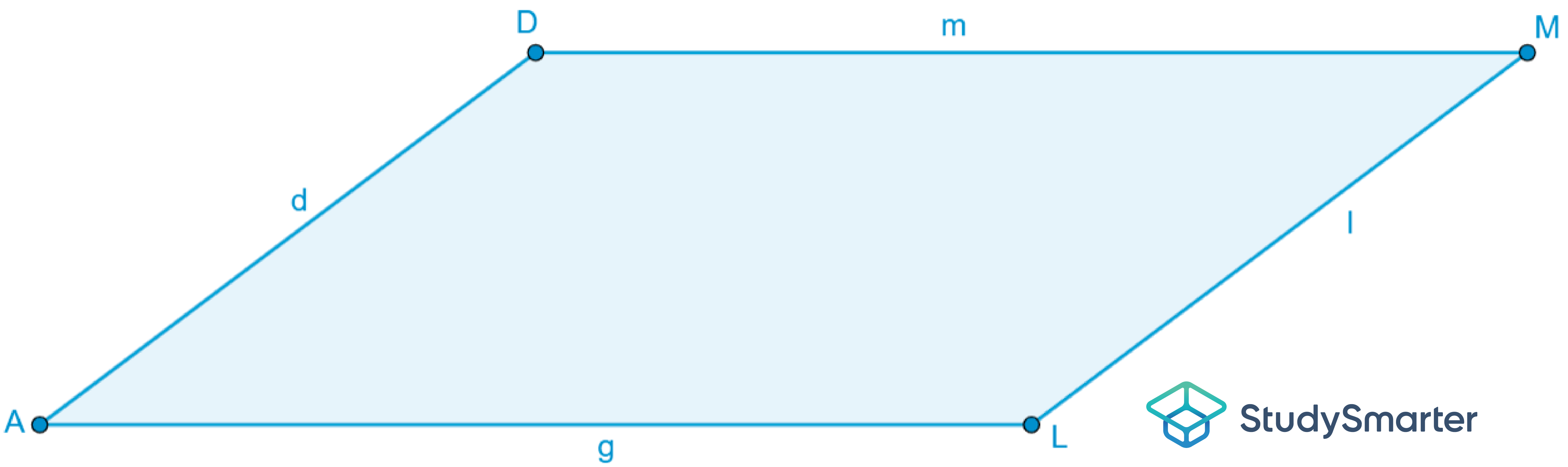
Ausbildung 
Karteikarten Erstelle und finde die besten Karteikarten.
Notizen Erstelle Notizen schneller als je zuvor.
Lernsets Alles was du brauchst an einem Ort.
Lernpläne Wöchentliche Ziele, Lern-Reminder, und mehr.
Spaced Repetition Nachhaltiger lernen.
AI powered learning Mithilfe unserer KI zum Lernerfolg
Blog 
