In diesem Artikel erfährst du alles, was du über die Berechnung des Schnittpunkts einer Geraden mit einer Ebene wissen musst. Immer wenn sich eine Gerade und eine Ebene im Raum befinden, die zueinander nicht parallel sind, dann schneiden sich diese. Dieser Schnitt kann entweder eine Gerade sein, die in der Ebene liegt oder ein einzelner Punkt, der auch Durchstoßpunkt genannt wird. Wie du diesen Punkt berechnen kannst, erfährst du in diesem Artikel.
Gerade und Ebene Grundlagenwissen
Erstmal solltest du dir diesen Abschnitt sorgfältig durchlesen, um die Grundlagen und Voraussetzungen abzuklären. Es ist wichtig zu wissen, wie eine Gerade im dreidimensionalem Raum mathematisch korrekt definiert ist.
Eine Gerade im dreidimensionalem Raum ist in Parameterform, wenn diese der folgenden Gleichung genügt:
Dabei ist 
der Stützvektor, 
der Richtungsvektor und 
eine beliebige reelle Zahl.
Dann solltest du auch wissen, wie eine Ebene im dreidimensionalem Raum definiert ist.
Eine Ebene im dreidimensionalem Raum ist in Koordinatengleichung bzw. Koordinatenform, wenn diese der folgenden Gleichung genügt:
Dabei sind a, b, c und d reelle Zahlen.
Eine Ebene im dreidimensionalem Raum ist in Parametergleichung bzw. Parameterform, wenn diese der folgenden Gleichung genügt:
Dabei sind r, s reelle Zahlen, 
der Stützvektor und 
,
die Richtungsvektoren der Ebene
Lagebeziehung Gerade Ebene Schnittpunkt
Es gibt drei verschiedene Fälle, wie sich eine Gerade zu einer Ebene im dreidimensionalem Raum verhalten kann. Eine Gerade kann die Ebene in einem Punkt schneiden, in der Ebene liegen oder parallel zur Ebene verlaufen. Grafisch kannst du dir das wie folgt vorstellen:
| Schnittpunkt |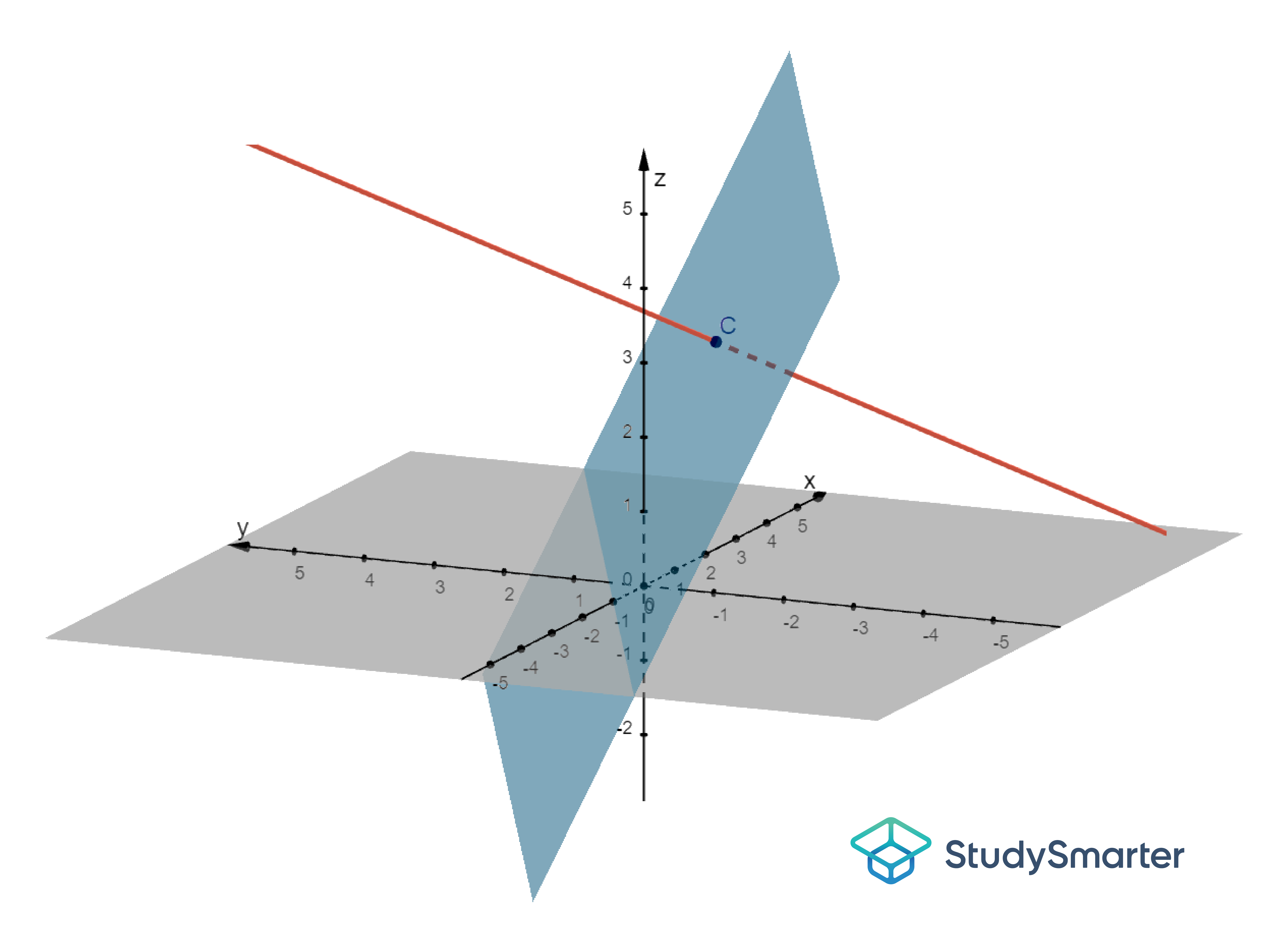 
Abbildung 1: Gerade schneidet die Ebene |
| Gerade liegt in der Ebene | 
Abbildung 2: Gerade liegt in der Ebene |
| Gerade liegt nicht in der Ebene, aber Gerade ist parallel zur Ebene |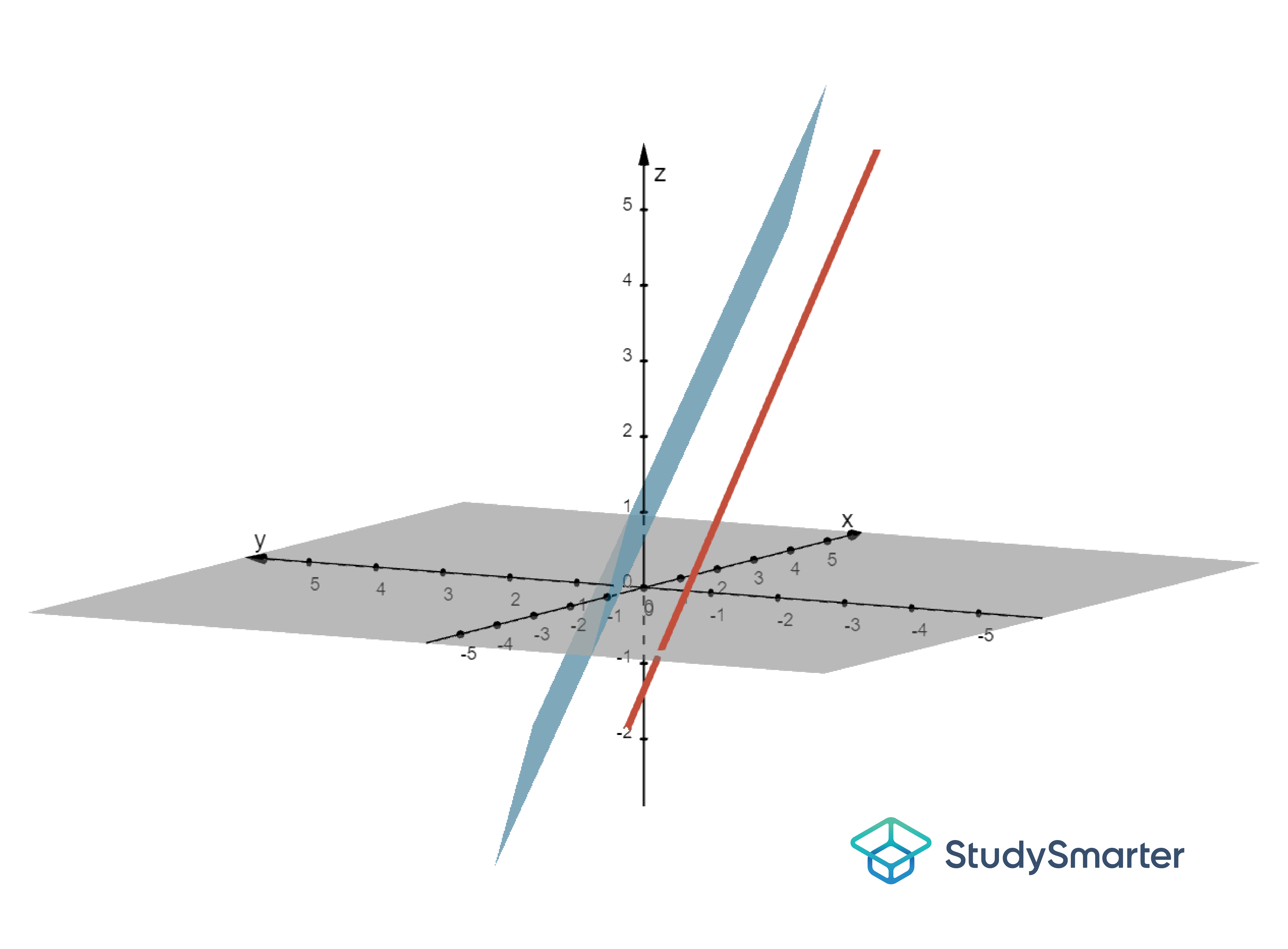 
Abbildung 3: Gerade verläuft parallel zur Ebene und schneidet diese nicht |
Falls dir das bis hierhin zu schnell war, dann solltest du dir am Besten den Artikel zur gegenseitigen Lage von Gerade und Ebene durchlesen!
In diesem Artikel widmen wir uns dem ersten Fall, so dass die Gerade die Ebene schneidet und der sogenannte Durchstoßpunkt bzw. Schnittpunkt ausgerechnet werden soll.
Schnittpunkt Gerade Ebene berechnen
Nachfolgend findest du Beispiele, wie du bei der Berechnung des Schnittpunktes zwischen einer Geraden und einer Ebene im dreidimensionalem Raum immer vorgehen kannst. Dabei schauen wir uns auch die unterschiedlichen Fälle, in der eine Ebene gegeben sein kann, an!
Schnittpunkt Gerade Ebene Koordinatenform
Falls die Ebene in Koordinatenform gegeben ist, dann erfolgt die Berechnung des Schnittpunkts relativ einfach. Nachfolgend findest du ein Beispiel mit Erklärungen. Nach diesem Beispiel kannst du dich orientieren, da die Schritte bei der Berechnung immer die Gleichen sind.
Aufgabe 1
Berechne den Schnittpunkt der Geraden g mit der Ebenen E
Lösung
1. Schritt: Stelle die Geradengleichung als lineares Gleichungssystem nach deren Koordinaten auf.
2. Schritt: Setze die Koordinaten in die Koordinatengleichung der Ebene ein.
3. Schritt: Vereinfache die entstandene Gleichung und löse nach Lambda auf.
4. Schritt: Nun setzt du Lambda in die Geradengleichung g ein und bestimmst damit den Schnittpunkt S.
Der Punkt indem sich die Gerade g und die Ebene E schneiden ist S(-1|-1|2).
Anschaulich kannst du dir die Aufgabe so vorstellen. Die hellblaue Ebene schneidet die orangene Gerade im Punkt S.
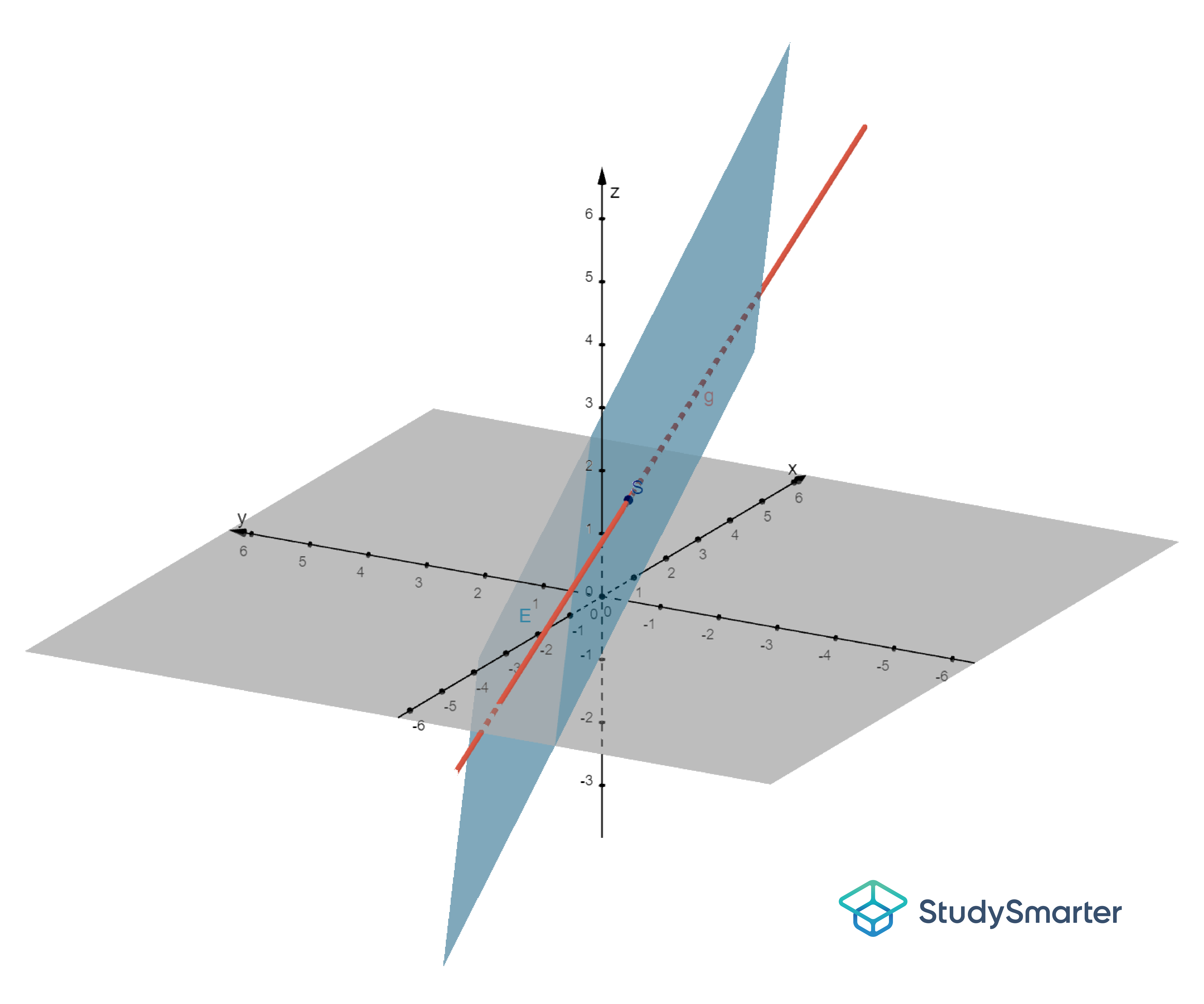
Abbildung 4: Schnittpunkt der Geraden g mit der Ebene E
Schnittpunkt Gerade Ebene Parameterform
Falls die Ebene in Parameterform gegeben ist, dann hast du zwei Möglichkeiten den Schnittpunkt zu berechnen.
- Transformiere die Ebene in Parameterform in Koordinatenform und verfahre wie oben
- Berechne den Schnittpunkt direkt
Wie du die verschiedenen Darstellungen der Ebenen umformst, kannst du im Artikel Ebenengleichung umformen nachlesen!
Zuerst schauen wir uns den zweiten Weg an. Dabei wird dir auffallen, dass die Rechenschritte etwas aufwendiger sind, als in der ersten Rechnung. Falls du damit aber keine Probleme hast, dann kannst du bei der Berechnung des Schnittpunkts immer so vorgehen.
Aufgabe 2
Berechne den Schnittpunkt der Geraden g mit der Ebenen E.
Lösung
1. Schritt: Stelle jeweils die beiden Darstellungsformen in ihrer Koordinatenform dar.
2. Schritt: Nun können die jeweiligen Variablen gleichgesetzt werden.
3. Schritt: Jetzt kannst du s und r in die dritte Gleichung einsetzen.
4. Schritt: Diese Gleichung kannst du vereinfachen und nach Lambda auflösen!
5. Schritt: Nun setzt du Lambda in die Geradengleichung g ein und bestimmst damit den Schnittpunkt S.
Der Punkt indem sich die Gerade g und die Ebene E schneiden ist S(-1|-1|2).
Vielleicht ist dir schon aufgefallen, dass dies der gleiche Schnittpunkt wie in dem vorherigen Beispiel ist und das ist auch so gewollt! Bei den beiden Ebenen handelt es sich um ein und dieselbe.
Da die Ebene die Gleiche wie im ersten Beispiel war, ist auch die Abbildung und der Schnittpunkt gleich wie oben.
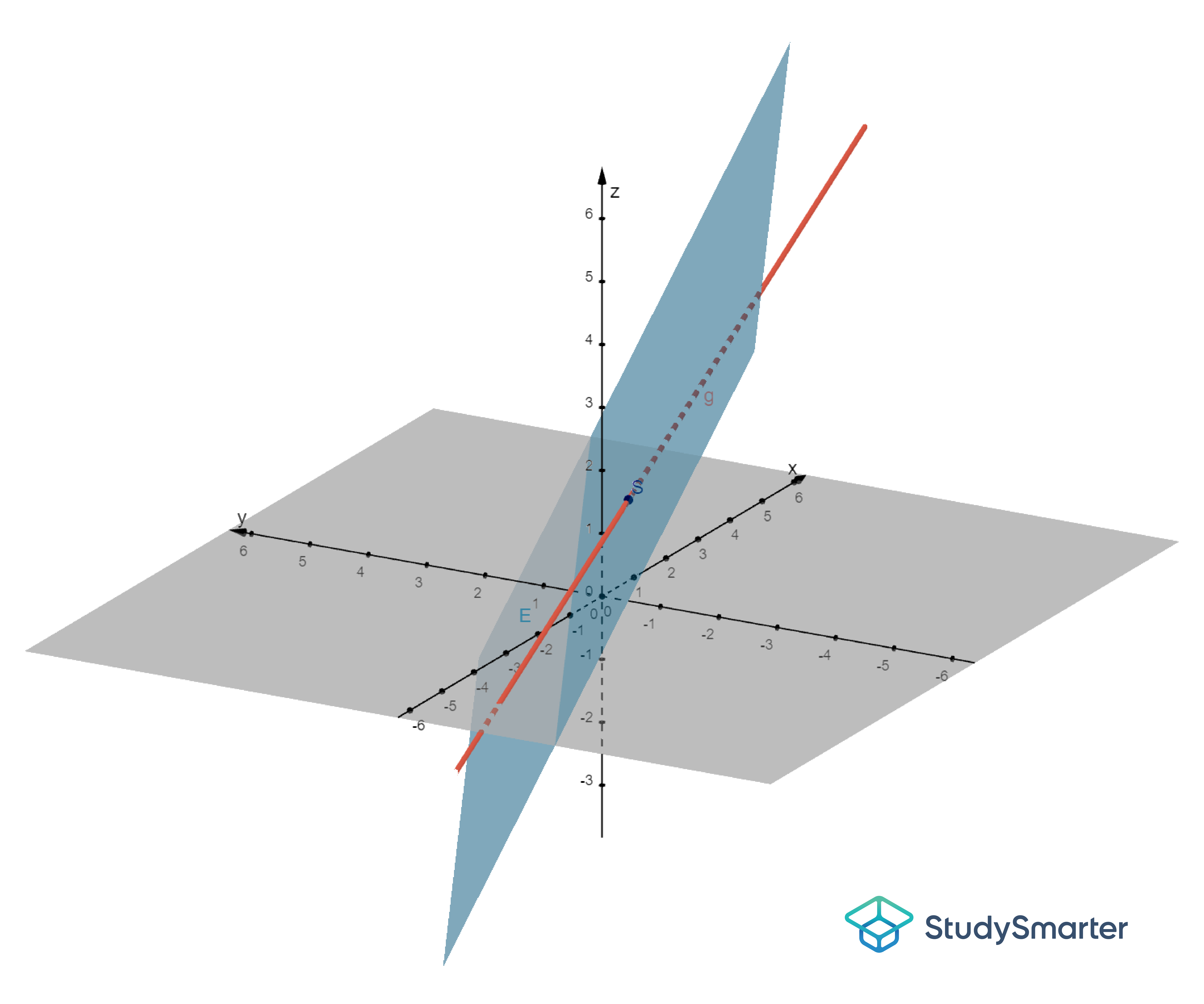
Abbildung 5: Schnittpunkt der Geraden g mit der Ebene E
Wenn du dir die unterschiedlichen Wege nicht merken möchtest bzw. dir das Umformen der Ebenen leichter fällt, dann ist der folgende Ansatz für dich!
Dazu wandelst du die Ebene in Parameterform in eine Ebene in Koordinatenform um.
Dazu schreibst du die Ebene erstmal in den entsprechenden Koordinaten als lineares Gleichungssystem.
Nun setzt du die ersten beiden Gleichungen in die zweite Gleichung ein.
Diese Gleichung stellst du dann nach der Zahl um, somit stehen die Variablen auf einer Seite.
Die Schritte der Berechnung des Schnittpunktes sind nun die Gleichen wie im ersten Beispiel!
Jetzt hast du alles zum Thema Schnittpunkt einer Gerade mit einer Ebene gelernt! Schau dir doch mal die dazugehörigen Karteikarten an, um dein Wissen direkt zu intensivieren!
Schnittpunkt Gerade Ebene - Das Wichtigste
- Wenn der Richtungsvektor nicht parallel zur Ebene steht, dann schneidet die Gerade die Ebene.
- Berechnung des Schnittpunkts entspricht dem Lösen eines linearen Gleichungssystems.
- Am einfachsten erfolgt die Berechnung, wenn die Ebene in Koordinatenform gegeben ist.
Erklärungen 
Magazine 
