Konfidenzintervall: Definition, Formel & Bedeutung

Q: Was sagt mir das Konfidenzintervall?

Das Konfidenzintervall (oder auch Vertrauensintervall) ist die Abschätzung eines Intervalls, in der ein festgelegter Parameter zu einer festgelegten Wahrscheinlichkeit (Konfidenzniveau) liegen soll.

Springe zu einem wichtigen Kapitel

Wenn Du auf ein Date gehst und nicht weißt, wie groß deine Verabredung ist, kannst Du anhand der statistischen Verteilung der Körpergröße die minimale und maximale Größe abschätzen. Alle zwischen diesen beiden Werten liegenden Körpergrößen sind Dein "Konfidenzintervall".

Konfidenzintervall – wichtige Definitionen

Das Konfidenzintervall wird dann gebraucht, wenn du einen wahrscheinlichen Parameter (z. B. Mittelwert der Körpergröße) aus einem großen Datensatz (alle Körpergrößen einer Zielgruppe) anhand mehrerer Stichproben abschätzen möchtest. Wie wahrscheinlich dieser geschätzte Mittelwert sein soll, bestimmst Du selbst.

Das Konfidenzintervall (oder auch Vertrauensintervall) ist die Abschätzung eines Intervalls, in der ein festgelegter Parameter zu einer festgelegten Wahrscheinlichkeit (Konfidenzniveau) liegen soll.

Es ist nicht das Intervall, in denen der Parameter mit der gegebenen Wahrscheinlichkeit liegt, sondern das Intervall, welches sich aus dem Schätzverfahren ergibt.

Das Konfidenzniveau ist eine wichtige Vorgabe, mit der Du festlegen kannst, wie genau oder wie tolerant Dein ausgerechnetes Konfidenzintervall zum Schluss ist.

Die Wahrscheinlichkeit, dass sich der festgelegte Parameter im bestimmten Konfidenzintervall befindet, heißt Konfidenzniveau (oder auch Überdeckungswahrscheinlichkeit oder Vertrauenswahrscheinlichkeit).

Das Konfidenzniveau wird im Vorfeld bestimmt und gibt dann an, wie tolerant Dein Intervall ist. Wenn die Wahrscheinlichkeit eines Treffers hoch sein soll, muss das Intervall entsprechend breit werden.

Möchtest Du, dass die Wahrscheinlichkeit, dass die korrekte mittlere Körpergröße in 19 von 20 Fällen im Konfidenzintervall liegt, ist das Konfidenzniveau 95 % .

$\frac{19}{20} = 0, 95 = 95 %$

Natürlich kann es passieren, dass die 95 % eben nicht eintreffen und Du Dich eben bei deiner Einschätzung der wahrscheinlichen Körpergröße irrst. Die Wahrscheinlichkeit dafür hat auch einen Namen.

Die Irrtumswahrscheinlichkeit ist die Wahrscheinlichkeit, mit der der festgelegte Parameter sich nicht im Konfidenzintervall befindet.

Diese ergibt sich dann einfach aus der Differenz des Konfidenzniveaus mit den maximal möglichen 100 %.

Die Irrtumswahrscheinlichkeit unseres Beispiels liegt bei 5 %.

$100 % - 95 % = 5 %$

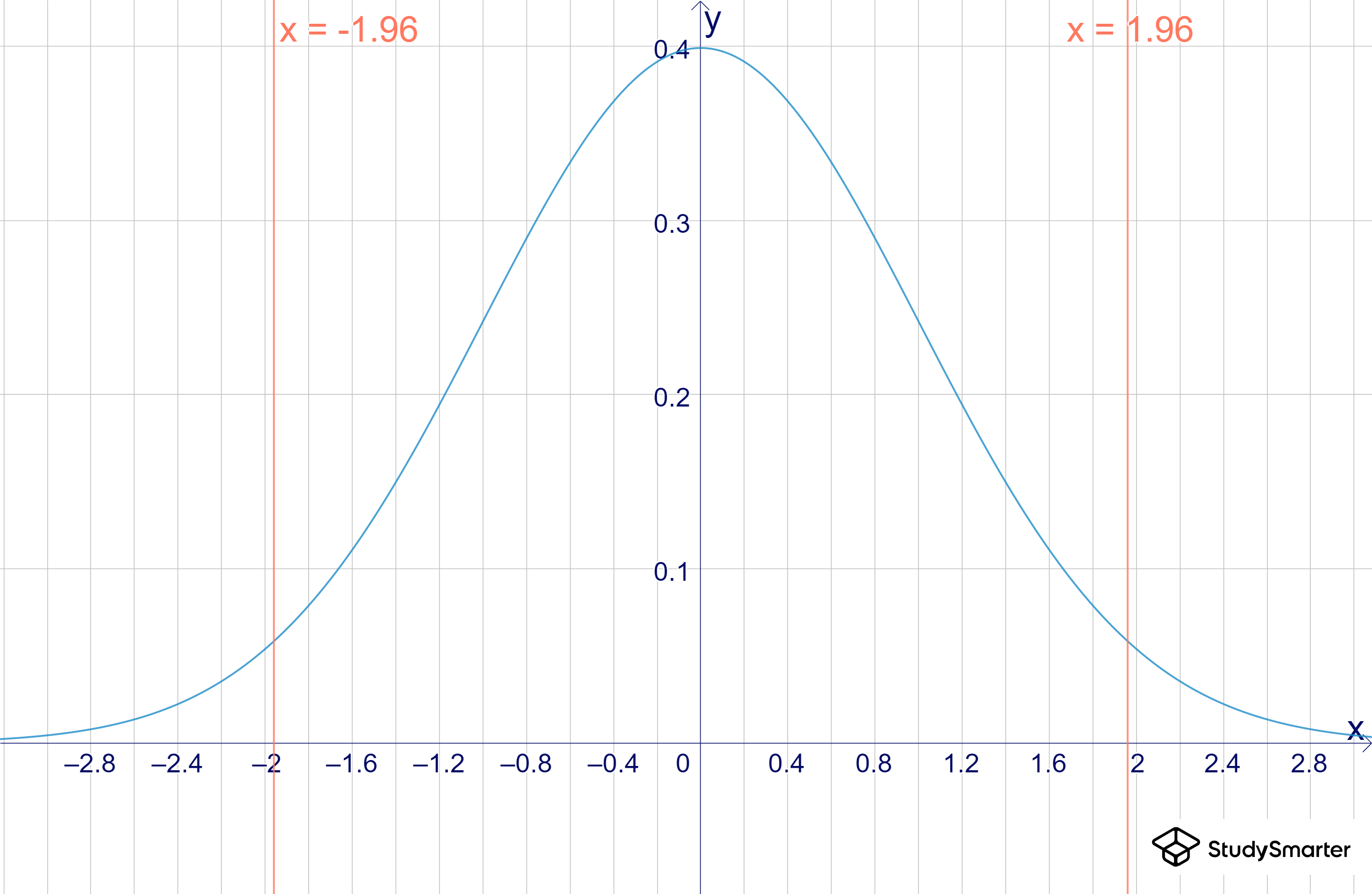
Konfidenzintervall 95 Konfidenzintervall StudySmarter

Abbildung 1: Konfidenzintervall zwischen -1,96 und 1,96

Die Wahrscheinlichkeit, dass der gesuchte Parameter zwischen den orangenen Strichen liegt, heißt Konfidenzniveau. Die Wahrscheinlichkeit, dass er im Bereich außerhalb ist, wird durch die Irrtumswahrscheinlichkeit bestimmt.

Das Konfidenzintervall wird durch zwei Werte begrenzt. Links ist die Untergrenze und rechts ist die Obergrenze.

Wenn man annimmt, dass die Körpergröße der möglichen Verabredungen gleichverteilt ist (was realistisch nicht der Fall ist), ist die Wahrscheinlichkeit, dass der wahre Wert unter der Untergrenze liegt, 2,5 % und dass er oberhalb der Obergrenze liegt, ebenso 2,5 %. Damit ergibt sich für die übrige Gesamtwahrscheinlichkeit wieder95 %.

$100 % - 2, 5 % - 2, 5 % = 95 %$

Konfidenzintervall – Formel

Wenn Du im Speziellen ein Konfidenzintervall für den Mittelwert berechnen möchtest, ergibt sich folgende Formel

$K I = x \pm z \cdot \frac{σ}{\sqrt{n}}$

Dabei ergibt sich der z-Wert aus dem Konfidenzniveau und der dazugehörigen Tabelle.

Standardabweichung σ und Stichprobengröße n ergeben sich aus der genommenen Stichprobe.

Du musst das Konfidenzintervall nicht um einen Mittelwert bestimmen, sondern kannst es um jede beliebige durchgeführte Punktschätzung durchführen. Dann setzt Du den geschätzten Punkt anstatt σ ein.

Wobei das "+" dann die Obergrenze und das "-" dann die Untergrenze ergibt.

Dabei sind:

$x$ : Mittelwert
z: z-Wert (des Konfidenzniveaus)
σ: Standardabweichung
n: Stichprobengröße

95 Konfidenzintervall Formel

Am häufigsten möchte man ein Konfidenzintervall von 95 % um den gesuchten Wert. Wenn man dieses dann wie oben um den Mittelwert bestimmen möchte, ergibt sich für das $z = 1, 96$ und damit für das gesamte Konfidenzintervall:

Konfidenzintervall Binomialverteilung

Beginnst Du Deine Suche mit einer Verteilung, die nicht (wie eine Normalverteilung) kontinuierlich ist, sondern nur aus einer Menge an einzelnen Bernoulli-Experimenten besteht, ist bei wenigen Stichproben die Rechnung von oben nicht anwendbar.

Bernoulli-Experimente sind Tests, die nur zwei Optionen zulassen: ja-nein, funktionsfähig-kaputt, gleich-ungleich.

Betrachtest Du nicht die genaue Körpergröße der Verabredung, sondern nur die Frage "Wird sie größer sein als ich?" (oder kleiner/gleich groß), dann hast Du keine durchgehende Verteilung mehr, die viele Optionen bietet, sondern nur noch zwei Optionen. "Ja" oder "Nein".

Bei sehr vielen Stichproben geht die Binomialverteilung in die Normalverteilung über und Du kannst die gleichen Formeln darauf anwenden.

Konfidenzintervall in der Normalverteilung berechnen

In den meisten Fällen, wenn Du ein konkretes Konfidenzintervall bestimmen sollst und Du nicht weißt, in welcher Verteilung die Messwerte gegeben sind, ist die Normalverteilung gemeint.

Als Erstes schaust Du nach, ob Du alle Werte hast, die Du benötigst und welche Du noch bestimmen oder herausfinden musst.

Mittelwert
Standardabweichung
z-Wert aus Konfidenzniveau
Konfidenzintervall KI bestimmen

1. Mittelwert ermitteln

Ist der Mittelwert nicht gegeben, musst Du ihn selbst bestimmen. Wenn Du zum Beispiel einen sehr großen Datensatz hast, nimmst Du eine (zufällige) Stichprobe und mittelst diese. Notiere Dir die Größe der Stichprobe n. Diese wird für die Standardabweichung im letzten Schritt benötigt. Ein möglichst guter Mittelwert ist besonders wichtig, denn um diesen baut sich Dein Konfidenzintervall auf. Er ist immer genau in der Mitte. Ist dieser Wert falsch, ist das Intervall falsch.

Den Mittelwert der Stichprobenwerte ermittelst Du, indem Du die Summe der Einzelwerte durch ihre Anzahl dividierst.

$x = \frac{\sum_{} x_{i}}{n}$

Deine bisherigen Erfahrungen der Körpergröße Deiner Dates waren 1,63 m; 1,58 m; 1,82 m; 1,77 m

Damit ergibt sich aus:

$\frac{(1, 63 + 1, 58 + 1, 82 + 1, 77)}{4} = 1, 70$

ein Mittelwert von $x = 1, 70 m$ .

2. Standardabweichung berechnen

Wie Du an die Standardabweichung σ kommst, kannst Du hier noch mal herausfinden.

Um die Standardabweichung zu berechnen, ziehst Du die Wurzel aus der Varianz. Die Varianz σ² ist definiert als die Summe der Quadrate der Differenzen zwischen Mittelwert $x$ und den einzelnen Werten der Messungen x_i (hier die Werte der Stichprobe), geteilt durch die Anzahl der Beobachtungen (hier die Stichprobengröße) n minus 1.

$σ^{2} = \frac{\sum {(x - x_{i})}^{2}}{n - 1}$

Damit ergibt sich für die Beispielgrößen deiner Stichprobe eine Varianz aus

$σ^{2} = \frac{{(1, 63 - 1, 7)}^{2} + {(1, 58 - 1, 7)}^{2} + {(1, 82 - 1, 7)}^{2} + {(1, 77 - 1, 7)}^{2}}{4 - 1} σ^{2} = 0, 1286$

Die Varianz ist die Summe der Quadrate der Differenzen zwischen all deinen Stichprobenwerten geteilt durch die Anzahl der Stichprobenwerte minus 1. Und daraus die Wurzel ergibt die gesuchte Standardabweichung.

$σ = \sqrt{\frac{\sum {(x - x_{i})}^{2}}{n - 1}}$

Ziehst Du aus der oben ermittelten Varianz die Wurzel, erhältst Du gerundet die Standardabweichung

$σ \approx 0, 113$

3. z-Wert aus Konfidenzniveau

Um den z-Wert zu bestimmen, musst Du die Verteilung, die Du momentan hast, mit dem gewünschten Konfidenzniveau in die Standardnormalverteilung transformieren.

Dafür gibt es Tabellen, aus denen Du diesen Wert zum gewünschten Niveau ablesen kannst.

Für das Eingangsbeispiel von 95 % ergibt sich dadurch, dass du auf beiden Seiten jeweils 2,5 % abziehst, der z-Wert $z = 1, 96$ .

Würdest du nur eine Sicherheit von 90 % anstreben, würde sich aus 2×5 % für 0,95 der z-Wert $z = 1, 645$ ergeben.

4. Konfidenzintervall Intervallschätzung

Für die Bestimmung des Konfidenzintervalls bei einer Normalverteilung benötigst Du für das Einsetzen in die finale Formel von oben:

$x$ : Mittelwert
z: z-Wert (des Konfidenzniveaus)
σ: Standardabweichung
n: Stichprobengröße

Der z-Wert stammt aus der Tabelle für z-Werte für das jeweilige Konfidenzintervall.

Bei 95 % (also jeweils 2,5 unter der Untergrenze und 2,5 % oberhalb der Obergrenze!) kannst Du $z = 1, 96$ aus der zugehörigen Tabelle ablesen.

Nun hast Du alle benötigten Werte bestimmt und kannst diese in die Formel einsetzen:

$K I = x \pm 1, 96 \cdot \frac{σ}{\sqrt{n}}$

Dann bleibt noch die Frage, was es mit dem Plus-Minus auf sich hat und wie aus einer Formel ein Intervall wird. Glücklicherweise kannst Du beide Fragen mit der gleichen Antwort lösen.

Ein Intervall hat eine Obergrenze, die sich aus der Formel mit dem Plus und eine Untergrenze, die sich aus der Formel mit dem Minus ergibt.

Also konkret:

$K I_{U n t e r g r e n z e} = x - z \cdot \frac{σ}{\sqrt{n}} K I_{O b e r g r e n z e} = x + z \cdot \frac{σ}{\sqrt{n}}$

Um jetzt also das Beispiel zu einem Ende zu führen, setzen wir alle Werte ein:

$K I = 1, 70 \pm 1, 96 \cdot \frac{0, 113}{\sqrt{4}}$

und erhalten für Unter- und Obergrenze des Konfidenzintervalls:

$K I_{U n t e r g r e n z e} = 1, 70 - 1, 96 \cdot \frac{0, 113}{\sqrt{4}} \approx 1, 59 K I_{O b e r g r e n z e} = 1, 70 + 1, 96 \cdot \frac{0, 113}{\sqrt{4}} \approx 1, 81$

Wenn Du Dich also beim Ausschau halten nach dem Date nur zu 5 % irren möchtest, kannst Du alle Personen oberhalb von 1,81 m und unterhalb von 1,69 m ignorieren und nur diejenigen mit der Körpergröße im Konfidenzintervall suchen.

Möchtest Du das Konfidenzintervall in Excel berechnen, kannst Du das auch über die finale Formel machen.

So schreibst Du einfach in die Zelle, in der die untere Grenze stehen soll:

=[Zelle des Mittelwertes]-[z-Wert deines Konfidenzniveaus]*([Zelle mit der Standardabweichung]/SQRT([Zelle der Probenanzahl]))

Konfidenzintervall Berechnung mit Excel StudySmarter Abbildung 2: Konfidenzintervall in Excel

In Abbildung 2 siehst Du, wie das Ganze mit konkreten Werten aussieht.

Interpretation des Konfidenzintervalls

Wenn Du jetzt die ermittelten Werte interpretieren möchtest, ist es hilfreich, noch mal einen Blick auf die Formel für das Konfidenzintervall und den Einfluss der darin enthaltenen Parameter zu werfen. Dabei achtest Du vorwiegend darauf, welche Werte rechts vom $\pm$ oberhalb und unterhalb des Bruchstrichs stehen.

$K I = x \pm z \cdot \frac{σ}{\sqrt{n}}$

Der Mittelwert $x$ (oder allgemeiner: Deine Punktschätzung), befindet sich immer in der Mitte, genau zwischen den beiden Grenzen. Der gesamte Teil der Formel rechts vom $\pm$ zeigt, wie breit das Intervall sein wird.

Sind Standardabweichung σ und z-Wert groß und n klein, wird das Konfidenzintervall sehr breit und ungenau, enthält aber umso sicherer den korrekten Wert.

Woher kommen die Werte also und wie genau kann man sie beeinflussen?

Der z-Wert kommt vom angestrebten Konfidenzniveau. Wenn Du Dir ganz sicher sein willst (99 % führt zu $2, 576$ ), dass der korrekte Mittelwert im angegebenen Intervall ist, muss das Intervall zwangsweise sehr groß werden, da der z-Wert mit dem Konfidenz-Niveau größer wird. Ein niedrigeres Konfidenzniveau (80 % hat $z = 1, 282$ ) sorgt entsprechend für ein schmaleres Intervall.

Die Standardabweichung (bzw. die Varianz) hängt vom Datensatz im Allgemeinen bzw. von der genommenen Stichprobe im Speziellen ab. Darauf hast Du also keinen so großen Einfluss. Hier ist auch klar, dass, wenn die Werte sehr stark schwanken (hohe Standardabweichung) auch die Verteilung und damit das Konfidenzintervall breiter werden muss.

Auf das n hast Du wieder insofern Einfluss, wenn Du einen gesamten, großen Datensatz da hast, aus dem Du selbst eine Stichprobe entnehmen kannst. Da das n unter dem Bruchstrich steht, kannst Du hier also mit mehr aufgenommenen Werten (größere Stichprobe) zu einem, kleineren Konfidenzintervall und damit einer höheren Wahrscheinlichkeit den korrekten Wert zu enthalten, kommen.

Parameteränderung	Folge
z-Wert/Konfidenzniveau werden größer	Konfidenzintervall wird breiter
Standardabweichung σ wird größer	Konfidenzintervall wird breiter
Stichprobe n wird kleiner	Konfidenzintervall wird breiter
z-Wert/Konfidenzniveau werden kleiner	Konfidenzintervall wird schmaler
Standardabweichung σ wird kleiner	Konfidenzintervall wird schmaler
Stichprobe n wird größer	Konfidenzintervall wird schmaler

Übungsaufgaben zum Konfidenzintervall

Hier siehst Du ein paar Beispielrechnungen, auf die Du treffen könntest.

Die erste Aufgabe ist eine Einfache zum Bestimmen und Einsetzen der korrekten Werte in die Formel.

Aufgabe 1

Du hast einen sehr großen Datensatz mit einem Mittelwert von $x = 80$ und berechnest eine Standardabweichung $σ = 10$ bei 200 von diesem Datensatz genommenen Daten. Von welcher Unter- bis zu welcher Obergrenze geht das Konfidenzintervall, in dem der Mittelwert zu 80 % (z-Wert 1,282) liegt?

Wenn Du in die Tabelle für die z-Werte zu der Standardnormalverteilung schaust, wird Dir auffallen, dass $z = 1, 282$ zu 0,9 gehört. Die fehlenden 0,1 sind auf jeder Seite einmal vertreten.

LösungFasse die Aufgabe zunächst in gegebene und gesuchte Größen zusammen:

Gegeben

Gesucht

Mittelwert

z-Wert

Standardabweichung

Stichprobengröße

x = 80

z = 1, 282

σ = 10

n = 200

Konfidenzintervall KI

Bei einem Blick in die Formel für das Konfidenzintervall:

$K I = x \pm z \cdot \frac{σ}{\sqrt{n}}$

fällt auf, dass alle Werte rechts vom Gleichheitszeiten gegeben sind. Du kannst diese direkt in Unter- und Obergrenze einsetzen:

$K I_{U n t e r g r e n z e} = 80 - 1, 282 \cdot \frac{10}{200} \approx 79, 1 K I_{O b e r g r e n z e} = 80 + 1, 282 \cdot \frac{10}{200} \approx 80, 9$

Anhand dieses Ergebnisses kannst Du auch sehen, wie sehr sich eine große Stichprobe und eine hohe Fehlertoleranz (niedrige angestrebte Treffsicherheit in Prozent) zu einem verhältnismäßig schmalen Konfidenzintervall führen. Wir können mit relativ großer Sicherheit sagen, dass der Mittelwert zwischen den beiden ausgerechneten Werten liegt.

In der zweiten Aufgabe kannst Du selbst aus einem Datensatz die Ausgangswerte ermitteln:

Aufgabe 2

Bestimme Unter- und Obergrenze für das 95 Konfidenzintervall folgender vier Messdaten einer Stichprobe:

$38; 72; 65; 25$

Lösung

Fang beispielsweise mit dem Mittelwert an. Die Definition für den Mittelwert lautet:

$x = \frac{\sum_{} x_{i}}{n}$

Die x_i hast Du oben alle einzeln gegeben und kannst einfach alle vier davon aufaddieren und einsetzen:

$x = \frac{38 + 72 + 65 + 25}{4} = 50$

Das z ergibt sich aus der gewünschten Größe für das Konfidenzintervall und ist laut Tabelle 1,96.

Die Standardabweichung σ ergibt sich wie oben gezeigt aus der Varianz σ².

Die gegebenen Werte eingesetzt in die Formel für die Varianz σ² ergeben:

$σ^{2} = \frac{\sum {(x_{i} - x_{i})}^{2}}{n - 1} = \frac{{(50 - 38)}^{2} + {(50 - 72)}^{2} + {(50 - 65)}^{2} + {(50 - 25)}^{2}}{4 - 1} = \frac{1478}{3} = 492, 6$

Die Standardabweichung kannst Du dann aus der Varianz (oder direkt mit der Wurzel in der Formel berechnen:

$σ = \sqrt{\frac{\sum {(x - x_{i})}^{2}}{n - 1}} = \sqrt{\frac{{(50 - 38)}^{2} + {(50 - 72)}^{2} + {(50 - 65)}^{2} + {(50 - 25)}^{2}}{4 - 1}} = \frac{\sqrt{4434}}{3} \approx 22, 2$

Und mit der Stichprobengröße $n = 4$ hast Du dann die vollständigen Formeln für Unter- und Obergrenze des Intervalls:

${K I}_{U n t e r g r e n z e} \approx 50 + 1, 96 \cdot \frac{22, 2}{\sqrt{4}} = 71, 756 {K I}_{O b e r g r e n z e} \approx 50 - 1, 96 \cdot \frac{22, 2}{\sqrt{4}} = 28, 244$

Die letzte Aufgabe ist eine Sachaufgabe, in der Du genau überlegen musst, welche vorkommende Zahl für welchen Teil im Term gilt:

Aufgabe 3

In einer Fabrik werden Nüsse nach Gewicht eingepackt. Der Leiter möchte, dass die angestrebte Gesamtzahl von 100 Nüssen pro Packung am Ende aber höchstens um 10 schwankt und dass höchstens 1 % der Verpackungen zu viele oder zu wenige Nüsse enthalten. Wie hoch darf die Standardabweichung bei 10 Stichproben höchstens sein?

Lösung

Nimm zuerst die Aufgabenstellung genau auseinander. Die angestrebte Gesamtzahl ist der Wert, um den man sich bewegt. Das ist also der Mittelwert $x$ .

Dieser soll um 10 schwanken, damit geht er von 90 bis 110. Alles, was da rausfällt, ist nicht im angestrebten Intervall. Also müssen das Unter- und Obergrenze für das Konfidenzintervall sein. Bei 1 % maximaler Fehlerquote haben wir in der Tabelle rechts und links jeweils einen halben Prozent, der fehlen darf. Das heißt, jeweils für Ober- und Untergrenze ergibt sich ein z-Wert von $z = 2, 576$ .

n ist die Stichprobenanzahl und sie liegt bei 30.

Gegeben

Gesucht

Mittelwert

z-Wert

Untergrenze

Obergrenze

Stichprobengröße

x = 100

z = 2, 576

= 90

= 110

n = 30

Standardabweichung

Beim Blick auf die zentrale Formel, zum Beispiel konkret für die Untergrenze,

$K I_{U n t e r g r e n z e} = x - z \cdot \frac{σ}{\sqrt{n}}$

wird klar, dass nur ein Wert (hier σ) gesucht wird und die anderen alle gegeben sind. Also musst Du nur die Formel umstellen, einsetzen und bist fertig!

Addiere also zuerst den Term mit dem gesuchten σ auf beide Seiten und subtrahiere die Untergrenze. Dann hast Du auf der linken Seite nur noch einen Bruch und ein Produkt um Deinen gesuchten Wert.

$z \cdot \frac{σ}{\sqrt{n}} = x - K I_{U n t e r g r e n z e}$

Jetzt musst Du nur noch durch z dividieren und mit $\sqrt{n}$ multiplizieren.

$σ = \frac{\sqrt{n}}{z} \cdot (x - K I_{U n t e r g r e n z e})$

Und jetzt, da Du eine finale Formel für den gesuchten Wert hast, musst Du nur noch einsetzen:

$σ = \frac{\sqrt{30}}{2, 576} \cdot (100 - 90)$

Und das ergibt dann exakt und gerundet für die erlaubte Standardabweichung jeweils:

$σ = \frac{5 \sqrt{30}}{1288} \approx 0, 213$

Du kannst als Übung für das Umstellen der Formel das Ganze nochmal für die Obergrenze durchführen. Du wirst auf die gleiche Standardabweichung kommen, da Du dann nicht Untergrenze von Mittelwert, sondern Mittelwert von Obergrenze abziehst und bei beiden die Differenz 10 ist.

Konfidenzintervall – Das Wichtigste

Ein Bereich der möglichen Ergebnisse einer Punktschätzung (meist ein Mittelwert).
Ist breiter, enthält den korrekten Wert aber wahrscheinlicher, wenn du das Konfidenzniveau (in Prozent) erhöhst.
Hat das Formelzeichen KI und die Formel KI = x±z·σnmit den Werten
- $x$ : Mittelwert
- z: z-Wert (des Konfidenzniveaus)
- σ: Standardabweichung
- n: Stichprobengröße.

Karteikarten in Konfidenzintervall 1

Lerne jetzt

Wann wird das Konfidenzintervall schmaler?

Wenn die Größe der Stichprobe größer wird.

Lerne mit 1 Konfidenzintervall Karteikarten in der kostenlosen StudySmarter App

Mit E-Mail registrieren

Du hast bereits ein Konto? Anmelden

Häufig gestellte Fragen zum Thema Konfidenzintervall

Was bedeutet 95 Prozent Konfidenzintervall?

Das 95 Prozent Konfidenzintervall ist der Bereich, in dem der gesuchte Parameter zu 95% zu finden ist. Das kann der Mittelwert eines großen Datensatzes oder eine beliebige Punktschätzung sein. Der z-Wert liegt dann bei 1,96.

Wann wird das Konfidenzintervall breiter?

Das Konfidenzintervall wird breiter, wenn die Standardabweichung der Stichprobe größer oder die Größe der Stichprobe kleiner wird. Außerdem wird es breiter, wenn das Konfidenzniveau, also die angestrebte Genauigkeit, und damit der z-Wert, größer wird.

Kann ein Konfidenzintervall negativ sein?

Nein. Ein Intervall ist ein Abstand zwischen einer unteren und einer oberen Grenze. Abstände sind immer größer Null.

Was sagt mir das Konfidenzintervall?

Das Konfidenzintervall (oder auch Vertrauensintervall) ist die Abschätzung eines Intervalls, in der ein festgelegter Parameter zu einer festgelegten Wahrscheinlichkeit (Konfidenzniveau) liegen soll.

Erklärung speichern

Entdecke Lernmaterialien mit der kostenlosen StudySmarter App

Kostenlos anmelden

Über StudySmarter

StudySmarter ist ein weltweit anerkanntes Bildungstechnologie-Unternehmen, das eine ganzheitliche Lernplattform für Schüler und Studenten aller Altersstufen und Bildungsniveaus bietet. Unsere Plattform unterstützt das Lernen in einer breiten Palette von Fächern, einschließlich MINT, Sozialwissenschaften und Sprachen, und hilft den Schülern auch, weltweit verschiedene Tests und Prüfungen wie GCSE, A Level, SAT, ACT, Abitur und mehr erfolgreich zu meistern. Wir bieten eine umfangreiche Bibliothek von Lernmaterialien, einschließlich interaktiver Karteikarten, umfassender Lehrbuchlösungen und detaillierter Erklärungen. Die fortschrittliche Technologie und Werkzeuge, die wir zur Verfügung stellen, helfen Schülern, ihre eigenen Lernmaterialien zu erstellen. Die Inhalte von StudySmarter sind nicht nur von Experten geprüft, sondern werden auch regelmäßig aktualisiert, um Genauigkeit und Relevanz zu gewährleisten.

Erfahre mehr

StudySmarter Redaktionsteam

Team Mathe Lehrer

14 Minuten Lesezeit
Geprüft vom StudySmarter Redaktionsteam

Erklärung speichern

Konfidenzintervall

StudySmarter Redaktionsteam

Konfidenzintervall – wichtige Definitionen