Weißt du, was genau ein Quadrat ausmacht? Um das herauszufinden, musst du dir nochmal kurz vor Augen führen, was ein Viereck überhaupt ist.
Einordnung Quadrat: Familie der Vierecke
Unter Vierecken versteht man geometrische Figuren, welche genau vier Ecken, folglich auch vier Seiten und vier Winkel aufweisen. Sie haben immer eine Innenwinkelsumme von 360°
Zählt man alle Winkel innerhalb des Vierecks zusammen, erhält man die sogenannte Winkelsumme.
Je nachdem, wie die Seiten angeordnet sind, unterscheidet man zwischen den folgenden Vierecken:
| Die Vierecksarten |
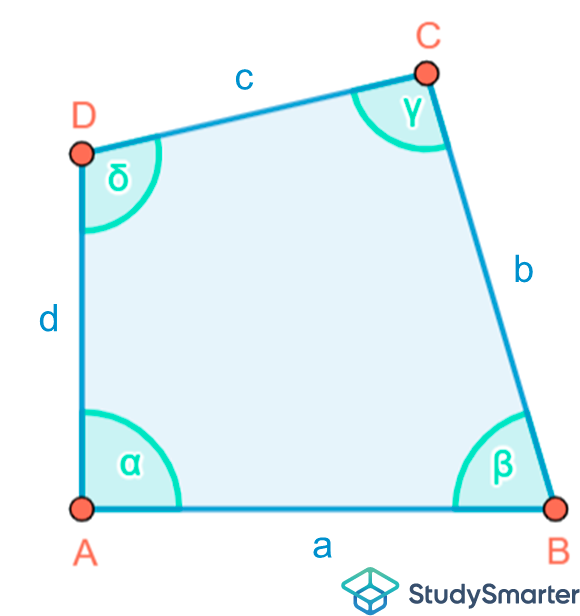
Abbildung 1: Allgemeines Viereck | 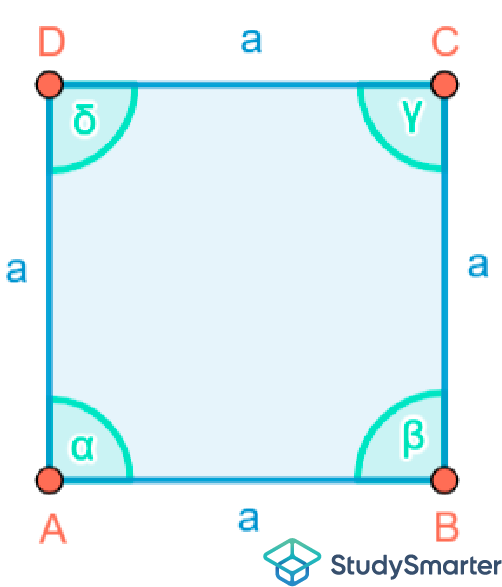
Abbildung 2: Das Quadrat | 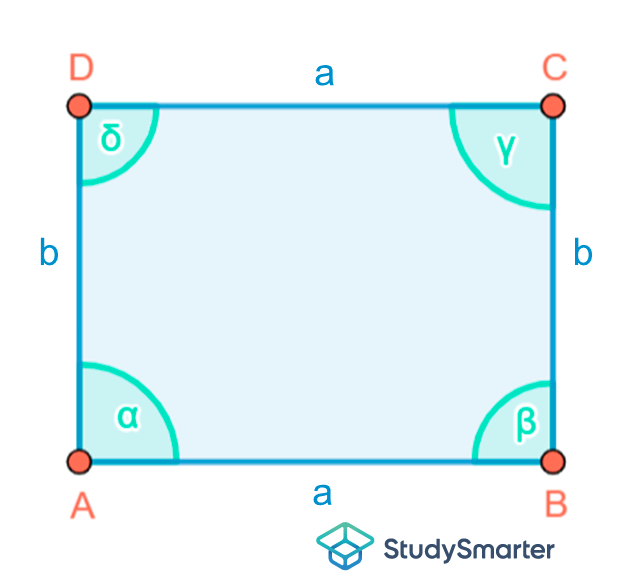
Abbildung 3: Das Rechteck | 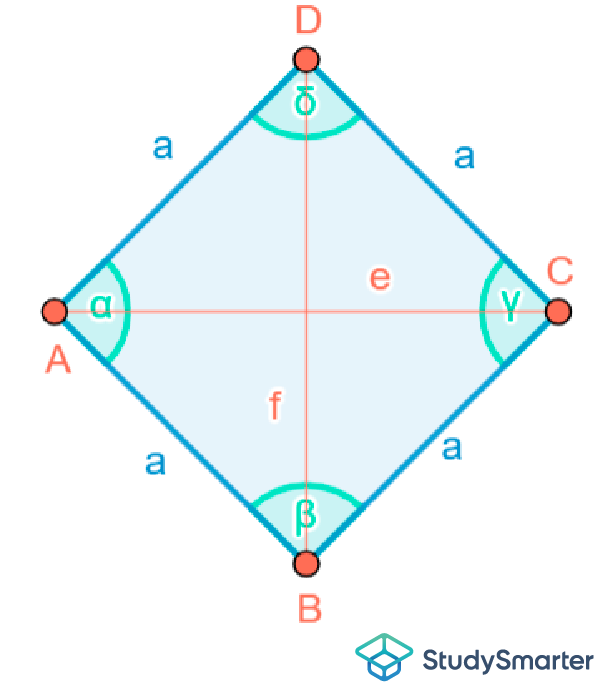
Abbildung 4: Die Raute |
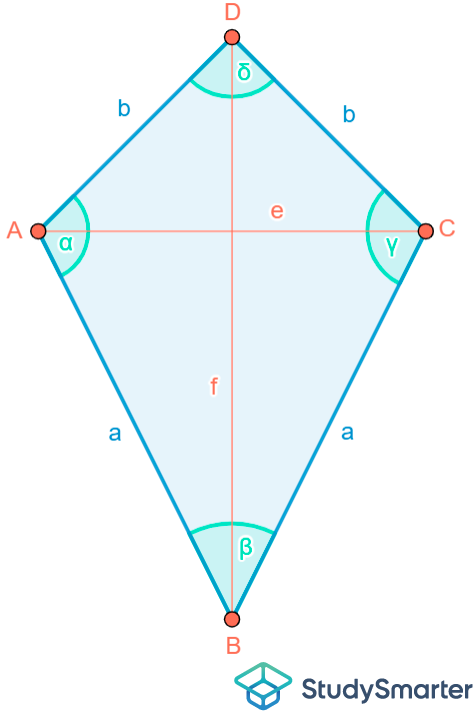
Abbildung 5: Der Drache | 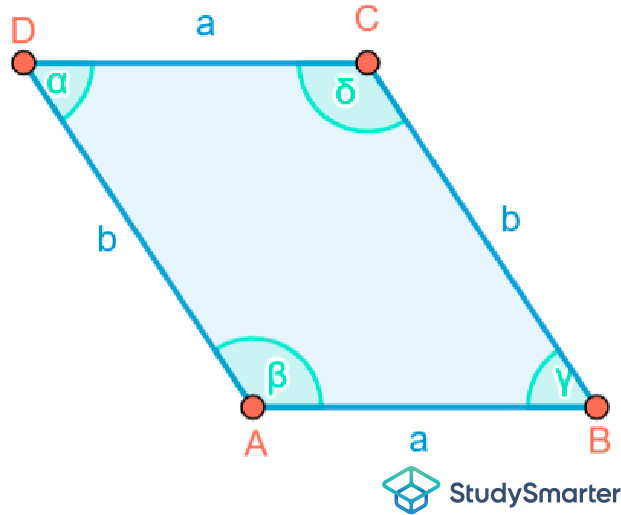
Abbildung 6: Das Parallelogramm | 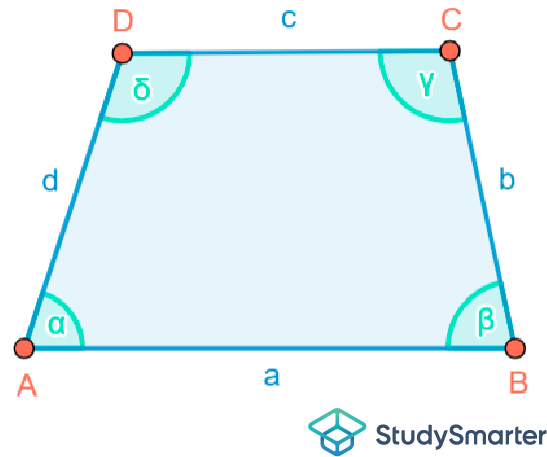
Abbildung 7: Das Trapez |
Die Seiten werden mit Buchstaben beschriftet, wobei jeder Buchstabe für einen konkreten Wert steht. Gleichlange Seiten haben also dieselbe Beschriftung.
Quadrat: Definition
Ein Quadrat gehört der Gruppe der Vierecke an und weist insgesamt vier gleich lange Seiten auf, wobei die jeweils gegenüberliegenden Seiten parallel zueinander stehen:
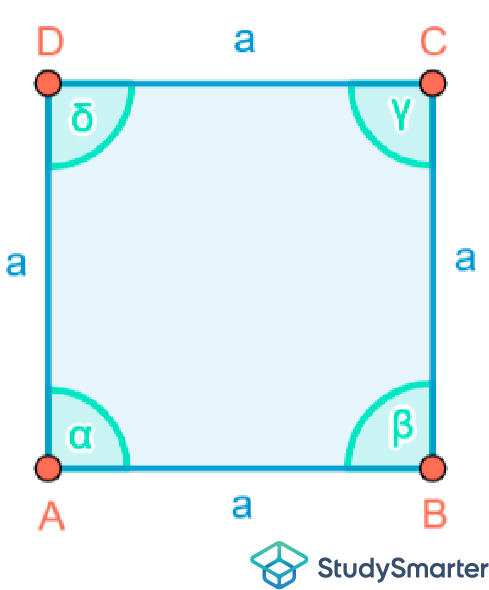
Abbildung 8: Das QuadratRechteck vs. Quadrat
Es gibt ein bestimmtes Merkmal, welches die beiden geometrischen Figuren grundlegend voneinander unterscheidet: Die Länge der Seiten. Beim Quadrat sind alle vier Seiten gleich lang. Beim Rechteck hingegen ist die Länge und die Breite der Figur unterschiedlich lang. Folgende Abbildungen der beiden Figuren sollen ein besseres Verständnis über deren Unterscheidung geben:
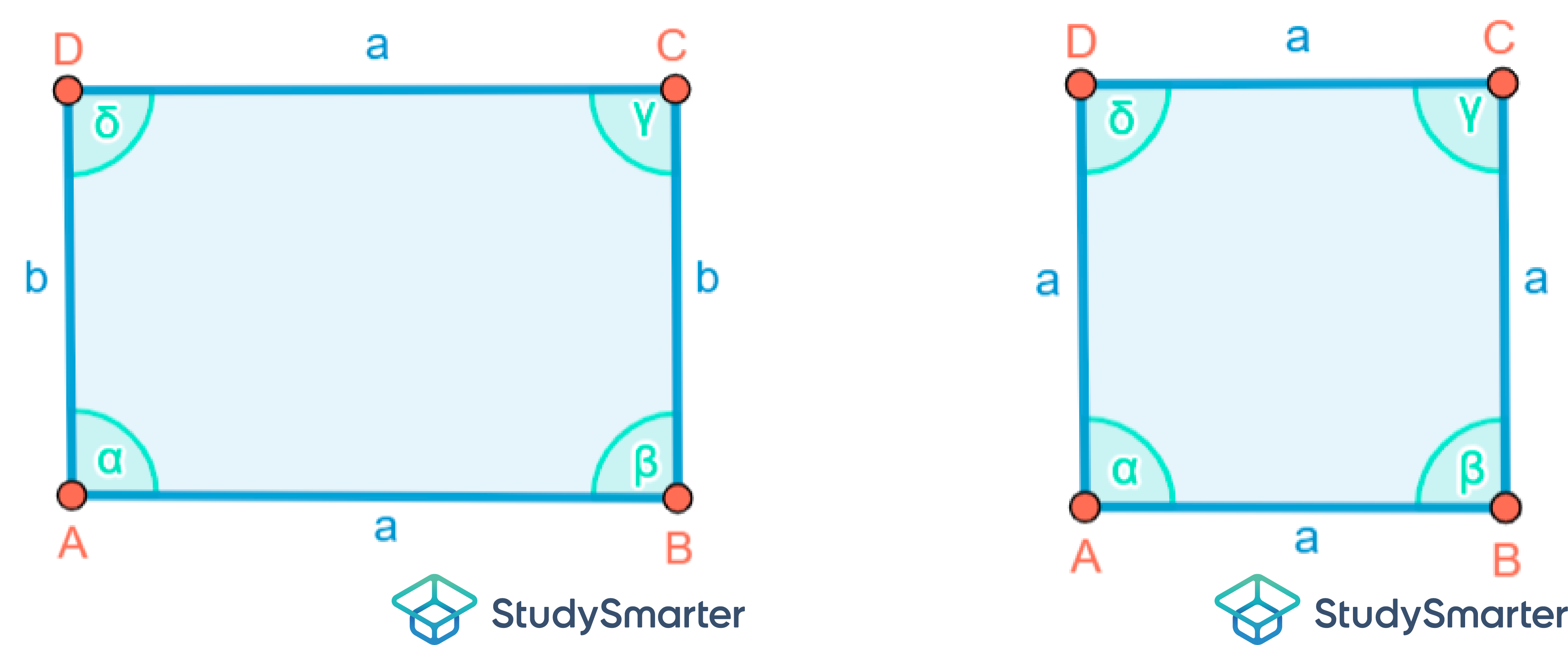
Abbildung 9: Das Rechteck. Abbildung 10: Das QuadratMöchtest du mehr über die geometrische Figur Rechteck erfahren? Dann sieh dir unseren dazugehörigen Beitrag dazu an!
Flächeninhalt Quadrat: Erklärung
In den folgenden Abschnitten lernst du, was genau eine Fläche ist, wozu man diese benötigt und wie man die Fläche eines Quadrats ausrechnen kann.
Was ist eine Fläche?
Unter einer Fläche versteht man eine zweidimensionale Ebene im Raum, welche aufzeigt, wie groß eine bestimmte Figur ist.
Was genau eine Fläche ist, zeigt dir das folgende Beispiel:
Aufgabe
Nimm dein kariertes Rechenheft zur Hand und schlage eine beliebige leere Seite auf. Hier siehst du zahlreiche Kästchen. Folgende Frage kommt hierbei auf:
"Wie viele Kästchen befinden sich eigentlich innerhalb meiner Zeichnung, wenn ich ein Quadrat zeichne, welches 6 Kästchen hoch und 6 Kästchen breit ist?"
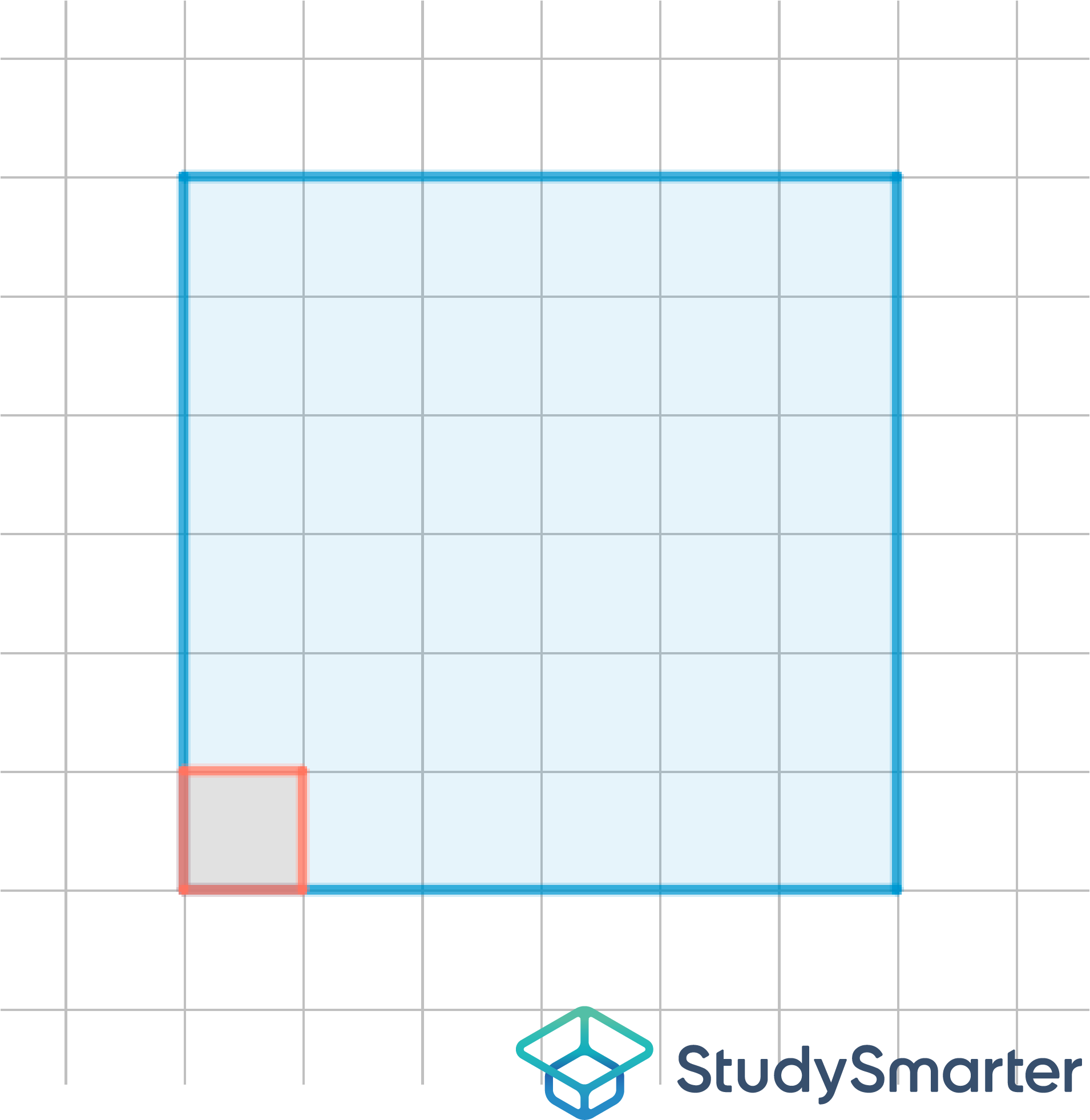
Abbildung 11: Skizze
Lösung
Zählst du nun händisch alle einzelnen Kästchen innerhalb der Zeichnung zusammen, dann erhältst du die Fläche des Quadrats, wobei Kästchen hierbei als Einheit für die Fläche verwendet werden. Wenn du richtig gezählt hast, sollten insgesamt 36 Kästchen innerhalb der von dir gezeichneten Figur als Ergebnis herauskommen.
Die Fläche ist also die Anzahl der Kästchen und gibt die Größe des Quadrats in "Kästchen" an.
Damit du nicht händisch zählen musst, gibt es eine Formel, mit welcher du die Fläche blitzschnell berechnen kannst.
Formel für die Flächenberechnung – Quadrat
Flächeninhalt eines Quadrats mit der Seitenlänge a:
Die Fläche wird in der Mathematik immer mit einem "A" und die Seiten des Quadrats mit "a" bezeichnet.
Überprüfen wir mit der Formel unser Beispiel von oben:
Bevor wir mit der Berechnung anfangen, machen wir uns immer eine kleine Skizze des Sachverhaltes bzw. der Aufgabenstellung. Gegeben haben wir unser Quadrat, dass wir mit einer bestimmten Kästchenanzahl gezeichnet haben:
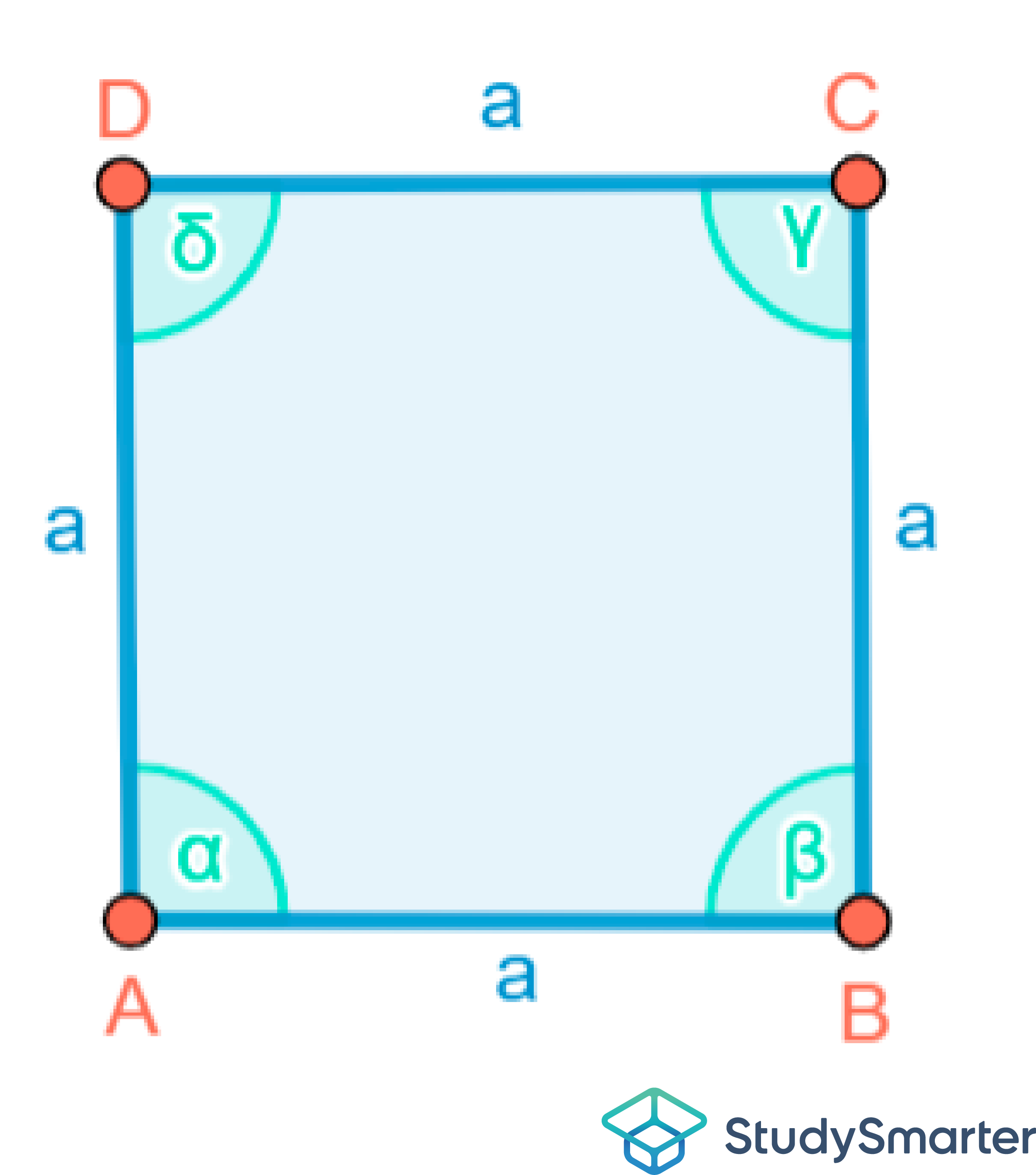
Abbildung 12: Skizze
Als Nächstes schreiben wir die Werte aus der Aufgabenstellung neben den jeweiligen Buchstaben, welcher für die Länge der Seiten der Figur steht. Hierbei gehen wir davon aus, dass die Seiten eines Kästchens einem halben Zentimeter entsprechen:
Nun müssen wir nur die Werte anstatt der Buchstaben in die Formel für die Berechnung des Flächeninhaltes des Quadrats einsetzen.
Multipliziert man nun diese beide Werte aus, erhält man oder 36 Kästchen. Warum sind diese beiden Werte unterschiedlich? Das liegt daran, dass die Seiten des Kästchens nur einen halben Zentimeter lang sind. Dadurch ergibt sich für die Fläche eines Kästchen ein anderer Wert:
Berechnen wir nun den Flächeninhalt des Quadrats mithilfe unserer 36 Kästchen, so erhalten wir:
Vergleichen wir diesen Wert mit dem, welchen wir beim händischen Zählen der Kästchen herausgekriegt haben, sehen wir, dass die beiden Werte übereinstimmen.
Wenn die Maßeinheit der Seiten der Figur einer Längeneinheit, also mm, cm, dm, m, km ist, musst du das Ergebnis der Fläche mit einem " ² "(hoch 2) nach deiner Längeneinheit versehen.
Umrechnungshilfe Einheiten
Wann du welche Einheit benutzen musst, siehst du in der folgenden Tabelle.
| Längeneinheit | Fläche |
| mm – Millimeter | mm² – Quadratmillimeter |
| cm – Zentimeter | cm² – Quadratzentimeter |
| dm – Dezimeter | dm² – Quadratdezimeter |
| m – Meter | m² – Quadratmeter |
| km – Kilometer | km² – Quadratkilometer |
Sehen wir uns zur Übung gleich noch ein weiteres Beispiel an:
Aufgabe
Gegeben ist folgender Wert eines Quadrats:
Berechne die Fläche des Quadrats.
Für die Berechnung ist es notwendig zu verstehen, was der Umfang eines Quadrats ist. Falls dir das nicht mehr ganz klar ist, lies einfach im entsprechenden Kapitel auf StudySmarter noch einmal nach.
Lösung
Als ersten Schritt fertigen wir immer eine kleine Skizze des Sachverhaltes ähnlich der Abbildung 13 an:
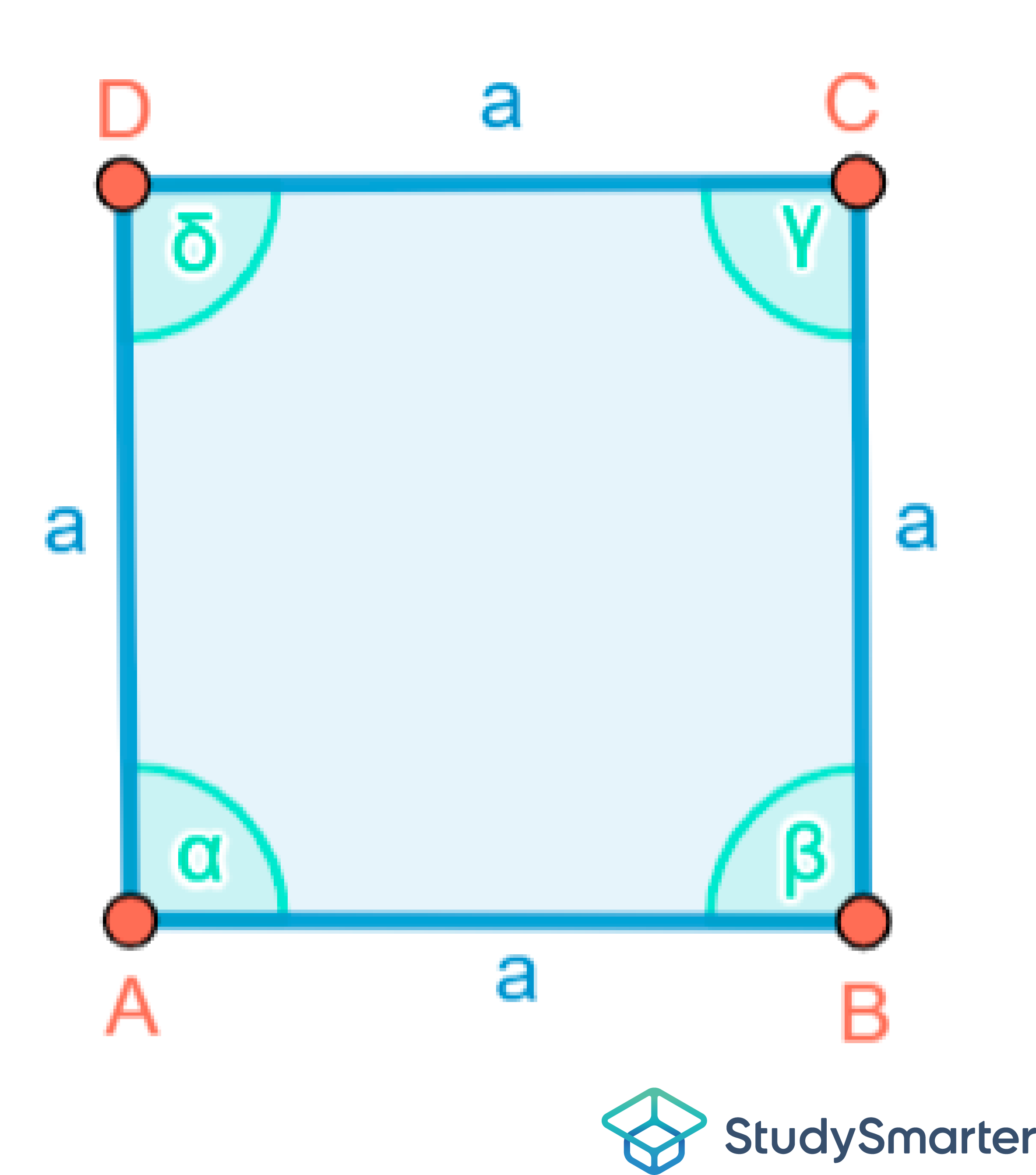
Abbildung 13: Skizze
Nun schreiben wir uns die Formel der Fläche des Quadrats nieder, welche wie folgt lautet:

Da wir für die Berechnung die Seite a benötigen, versuchen wir, mithilfe des gegebenen Wertes, also des Umfangs, auf unsere Seite a schließen zu können.
Gegeben ist der Umfang, welchen wir durch das Zusammenzählen aller Seiten berechnen. Wenn wir auf unsere Skizze schauen, wird klar, dass die Formel des Umfangs lautet:

Wie wir in der Formel sehen können, befindet sich dort ein a. Das bedeutet, dass wir die Formel nach a freistellen können, indem wir die 4 mit dem Gegenoperator der Multiplikation, also der Division, auf die andere Seite schieben:

Da wir die Seitenlänge a nun ausgerechnet haben, können wir dessen Wert nun in die Flächenformel einsetzen:

Die Fläche des Quadrats beträgt also .
Aufgabe
Die Diagonale eines Quadrats beträgt .
Berechne die Fläche.
Um diese Aufgabe lösen zu können, ist es notwendig, sich zuvor den hier verlinkten Beitrag zum Satz des Pythagoras anzusehen.
Lösung
Als ersten Schritt fertigen wir eine Skizze des Sachverhaltes an:
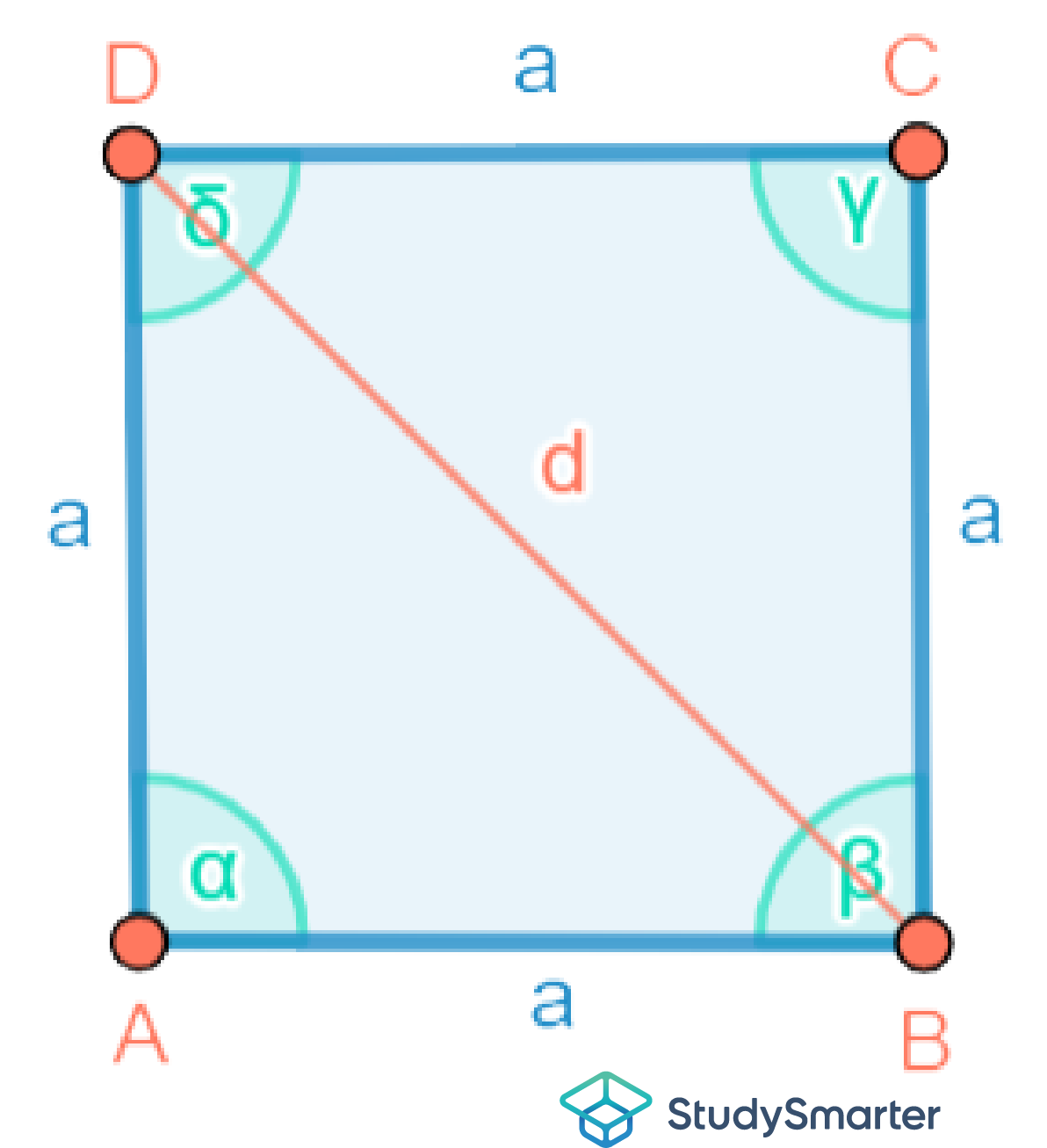
Abbildung 14: Skizze
Da wir für die Berechnung der Fläche die Seitenlänge a benötigen, müssen wir versuchen von der Diagonale auf die Seite schließen zu können. Genau hierbei kommt der Satz des Pythagoras ins Spiel:
Unter und versteht man die kürzeren Seiten im rechtwinkligen Dreieck, welches in Abbildung 15 dargestellt wird. Die Hypotenuse H stellt die Diagonale dar:
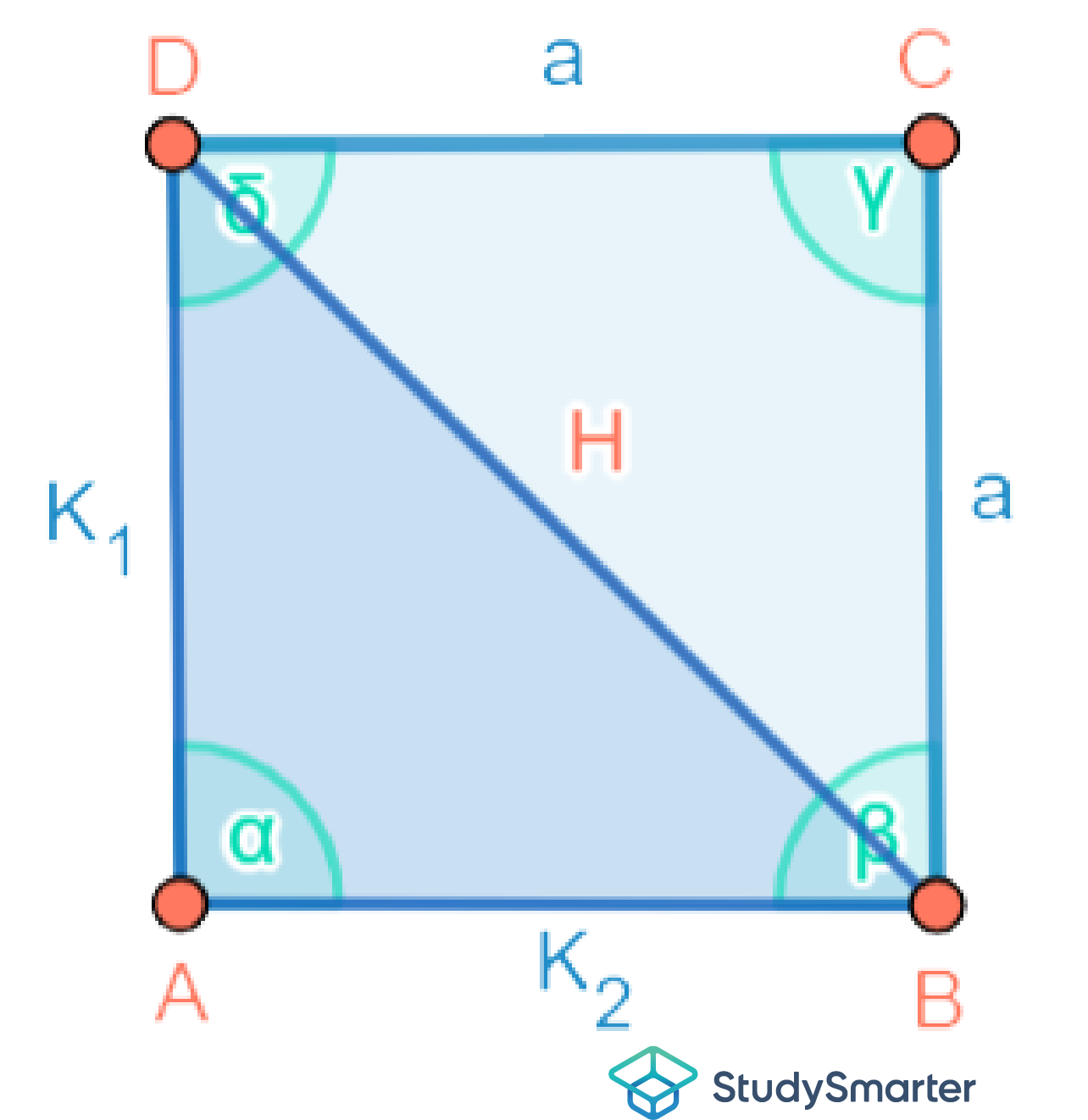
Abbildung 15: Skizze
Setzen wir nun unsere Werte bzw. Buchstaben in die Formel ein, sieht dies wie folgt aus:
Da wir nun die Seitenlänge a bestimmt haben, können wir den Wert in die Formel für die Flächenberechnung einsetzen:

Die Fläche des Quadrats beträgt also .
Mit der folgenden Übungsaufgabe kannst du dein Wissen überprüfen:
Aufgabe
Eine quadratische Wiese hat insgesamt eine Fläche von . Berechne die Länge der Seiten der Wiese.
Lösung
Als ersten Schritt fertigen wir uns eine Skizze des Sachverhaltes wie in Abbildung 16 an:
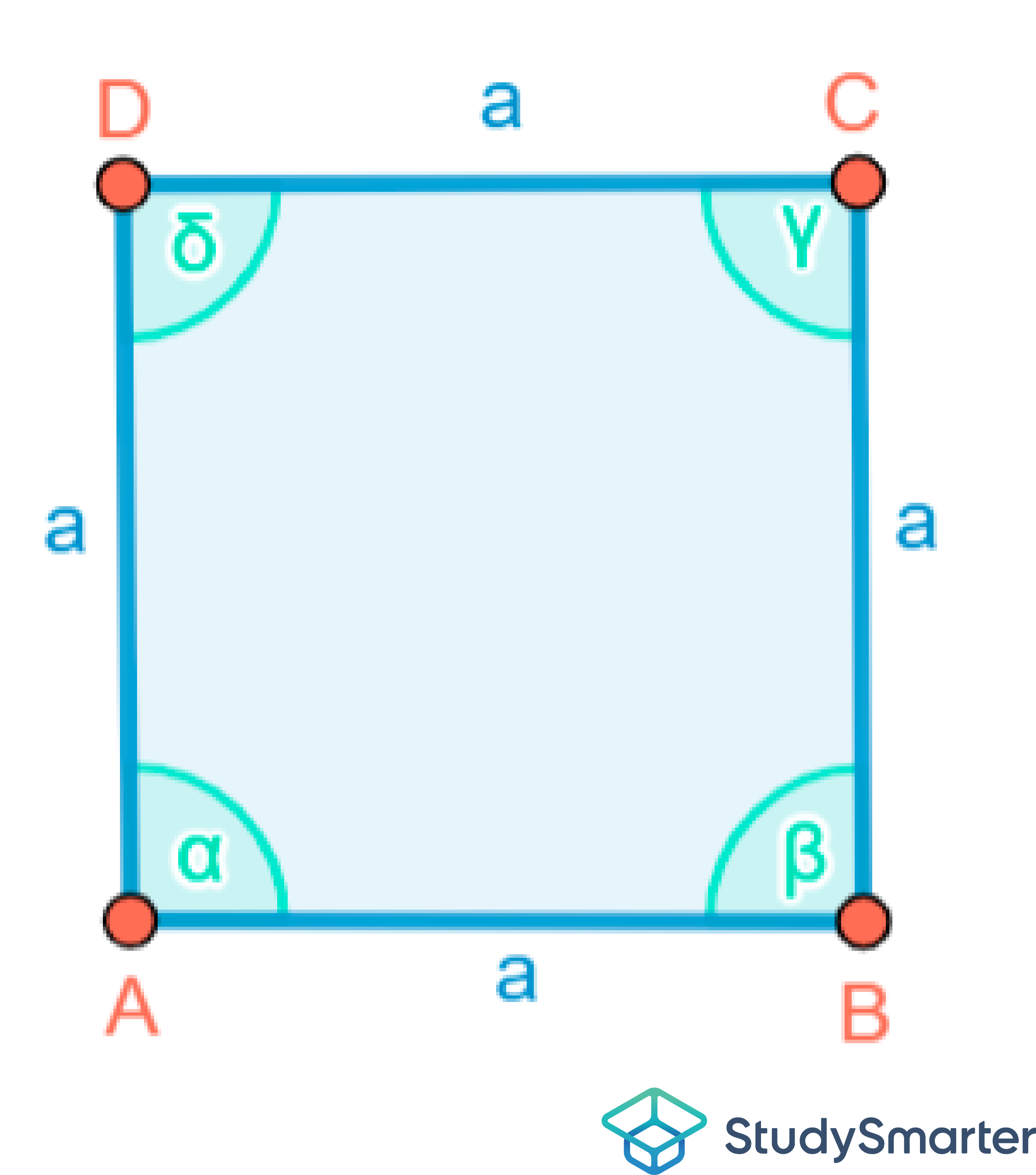
Abbildung 16: Skizze
Als Nächstes schreiben wir die allgemeine Flächenformel für das Quadrat hin und setzen die uns bekannten Werte ein:
Nachdem wir nun die gegebene Zahl für die Fläche eingesetzt haben, müssen wir diese Formel nach dem gesuchten Wert a auflösen, indem wir beim Quadrat die Quadratwurzel des Wertes der Fläche ziehen. Als Ergebnis erhalten wir somit:
Als Lösung für diese Aufgabe erhalten wir also eine Seitenlänge der Wiese von .
Flächeninhalt Quadrat - Das Wichtigste
- Ein Viereck erkennst du daran, dass es vier Winkel, vier Ecken und vier Seiten aufweist.
- Beim Quadrat sind alle vier Seiten gleich lang, alle Winkel genau 90° und jeweils zwei Seiten parallel zueinander.
- Die Flächenformel des Quadrats lautet: .
- Die Umfangsformel lautet:
 .
. - Die Seitenformel bei gegebener Fläche lautet:
 .
. - Die Seitenformel bei gegebenem Umfang lautet:
 .
.
























 .
. .
. .
.


