Allgemeines Dreieck
Damit du in Zukunft blitzschnell erkennen kannst, ob es sich bei einer Figur um ein Dreieck handelt oder nicht, zeigen wir dir wie ein allgemeines Dreieck aussieht. Das kannst du in Abbildung 1 erkennen.
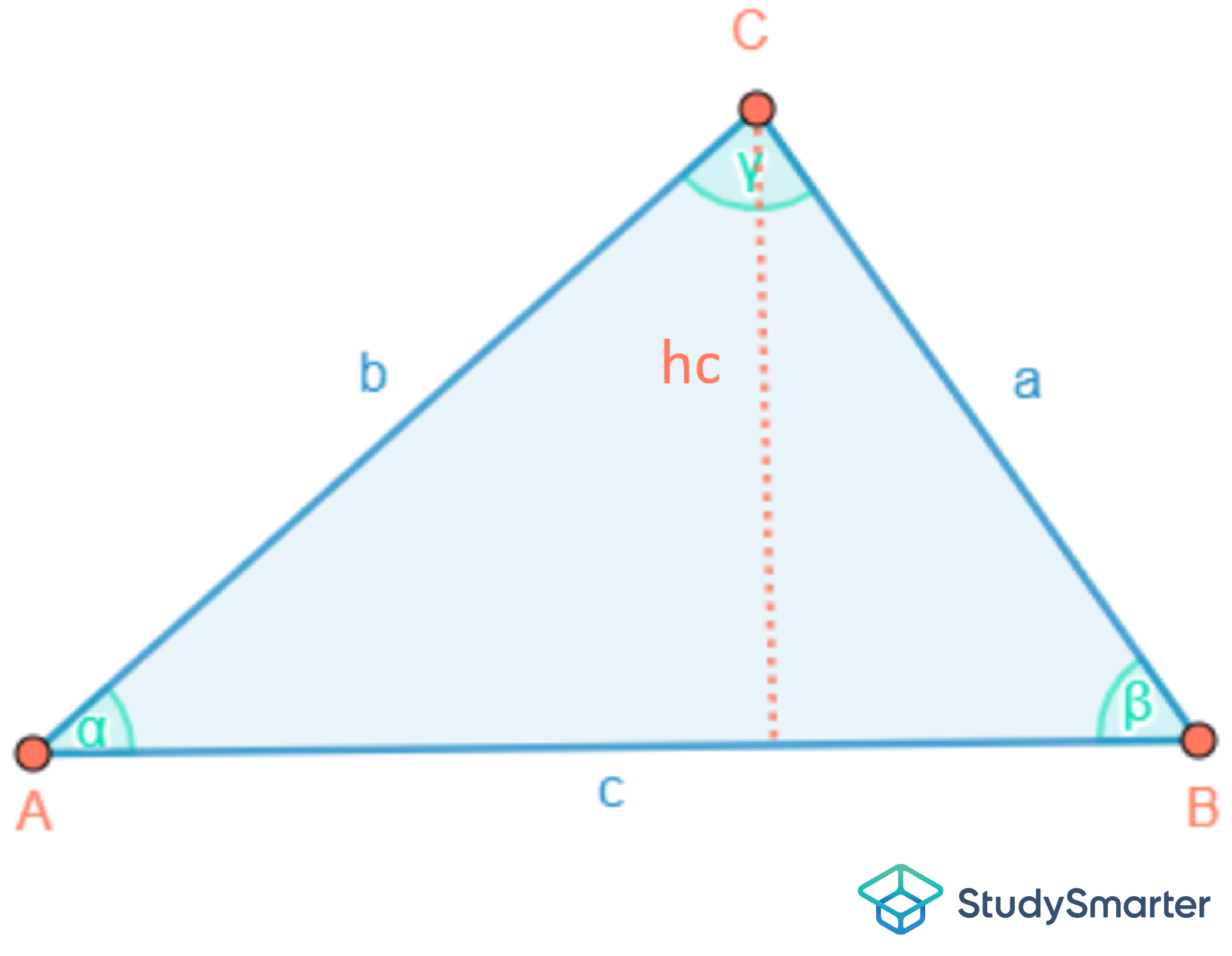
Abbildung 1: Allgemeines
DreieckSolltest du bei Hausübungen ein Dreieck zeichnen müssen, dann musst du dich bei der Beschriftung an wichtige Regeln halten, die wie folgt lauten:
Die Eckpunkte werden entgegen dem Uhrzeigersinn mit Großbuchstaben (beginnend bei A in der linken Ecke) beschriftet.
Die Seiten des Dreiecks werden wie ihr gegenüberliegender Eckpunkt bezeichnet, jedoch als Kleinbuchstaben.
Die Winkel werden wie die Eckpunkte entgegen dem Uhrzeigersinn beschriftet, jedoch mit griechischen Buchstaben aus dem griechischen Alphabet, beginnend bei Alpha. Das heißt der Winkel Alpha ist dort, wo der Eckpunkt A ist.
Hier findest du eine kurze Übersicht über die Zusammenhänge der Bezeichnung der Eckpunkte, der Seiten und deren Winkel:
| Eckpunkte | Winkel | Seiten |
| A |  | a |
| B |  | b |
| C |  | c |
Die drei Winkel ergeben zusammen im Dreieck immer eine Summe von 180°. Dies wird auch als Winkelsumme bezeichnet.
Ein Dreieck kann verschiedenste Seitenlängen oder Größen der Winkel aufweisen, was auch bedeutet, dass diese immer anders aussehen und verschiedene Eigenschaften haben können. Deshalb unterscheidet man die folgenden sechs Dreiecksarten, um einen besseren Überblick schaffen zu können.
Dreiecksarten
Die folgende Übersicht wird dir bestimmt helfen, in Zukunft jedes Dreieck seiner Art perfekt zuordnen zu können. Dreiecke werden nach zwei verschiedenen Merkmalen kategorisiert:
- Der Seitenlänge
- Den größten Winkel
Schauen wir uns die verschiedenen Dreiecke einmal an, die es so gibt.
| Dreiecksarten nach Seitenlänge |
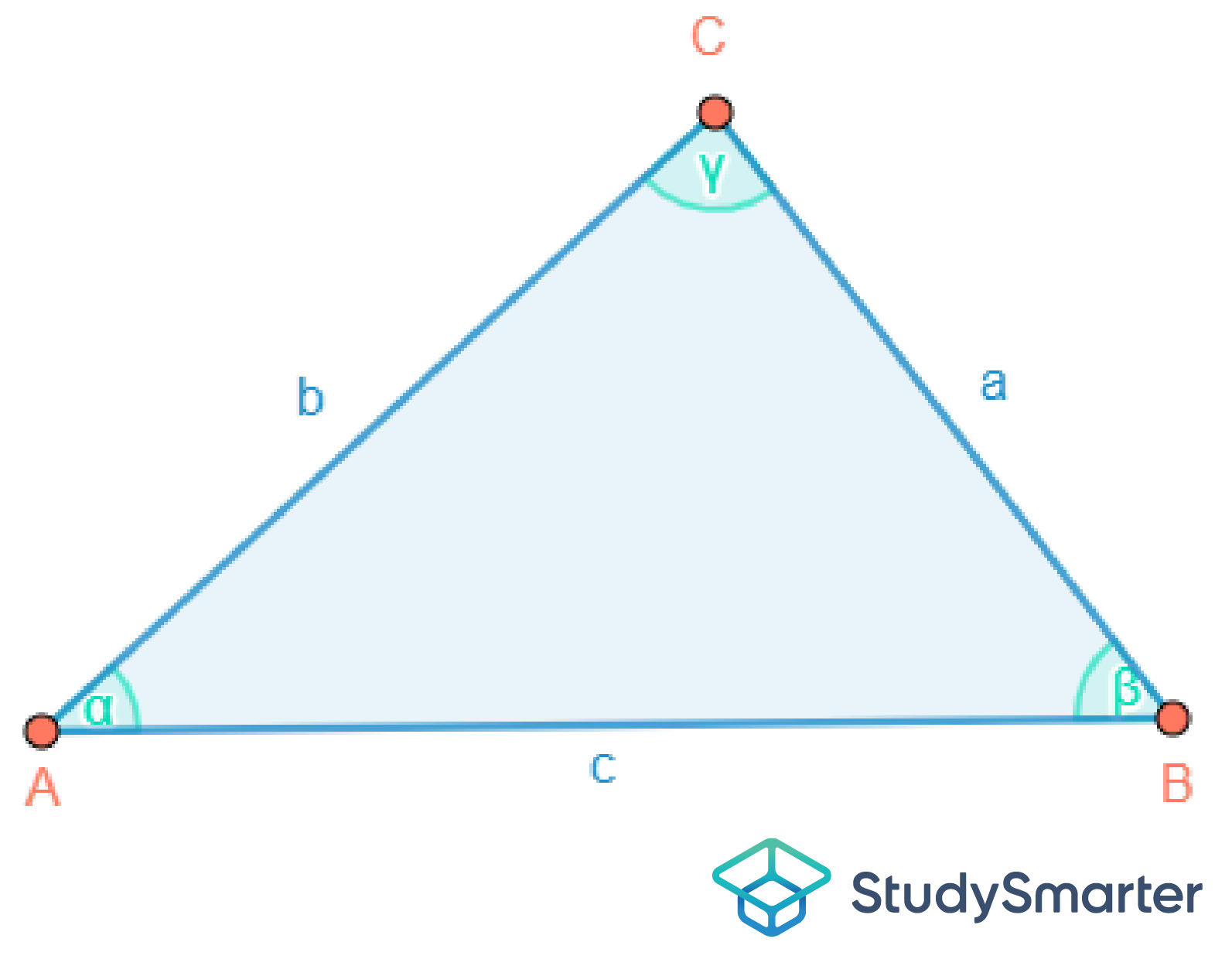
Abbildung 2: Allgemeines Dreieck | 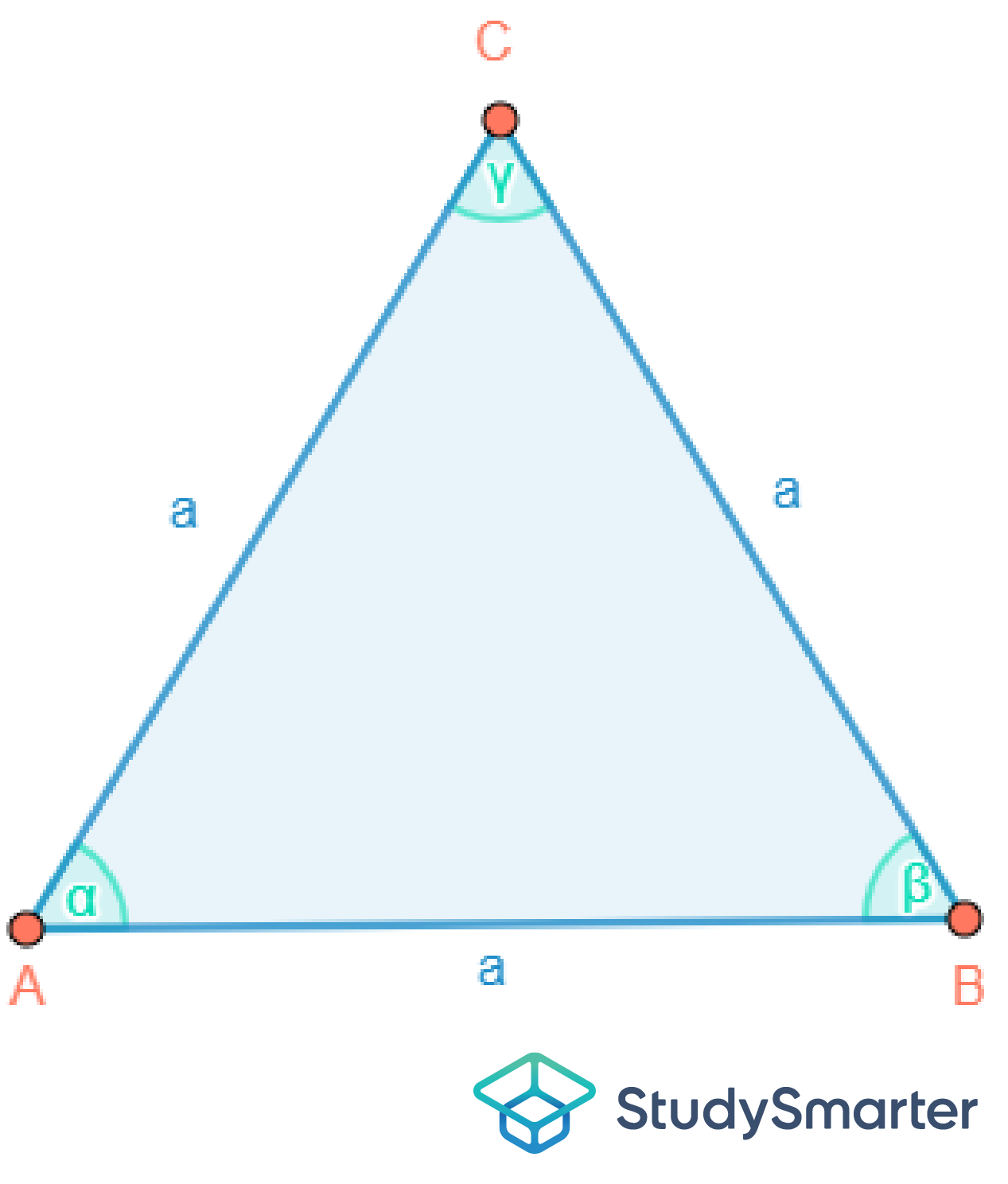
Abbildung 3: Gleichseitiges Dreieck | 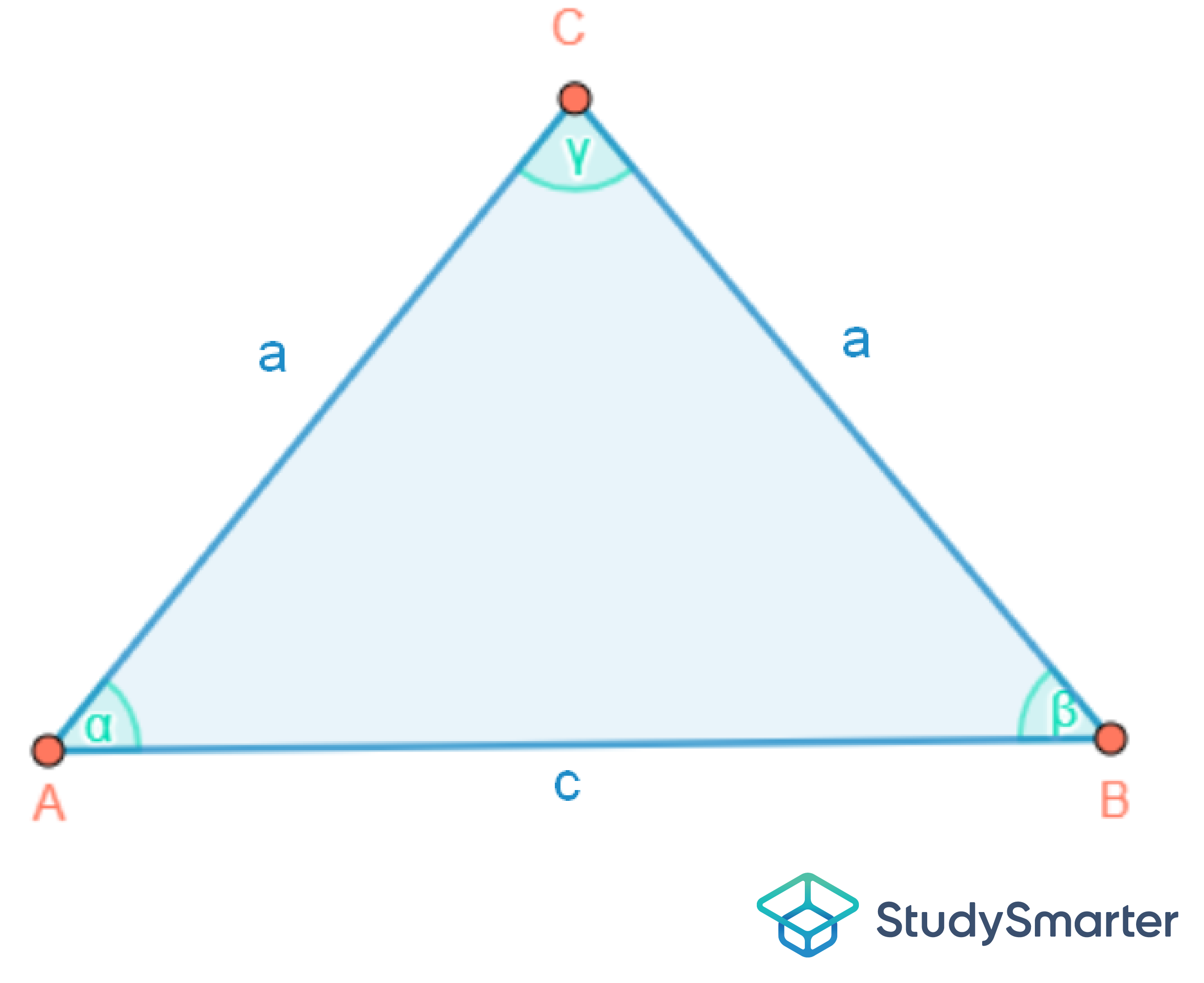
Abbildung 4: Gleichschenkliges Dreieck |
Wenn mehrere Seitenlängen mit dem gleichen Buchstaben beschriftet werden, dann handelt es sich hierbei um gleich lange Seiten. Dies ist ein schneller Weg, um herauszufinden, wie viele Seiten eines Dreiecks gleich lang sind.
| Dreiecksarten nach Winkel |
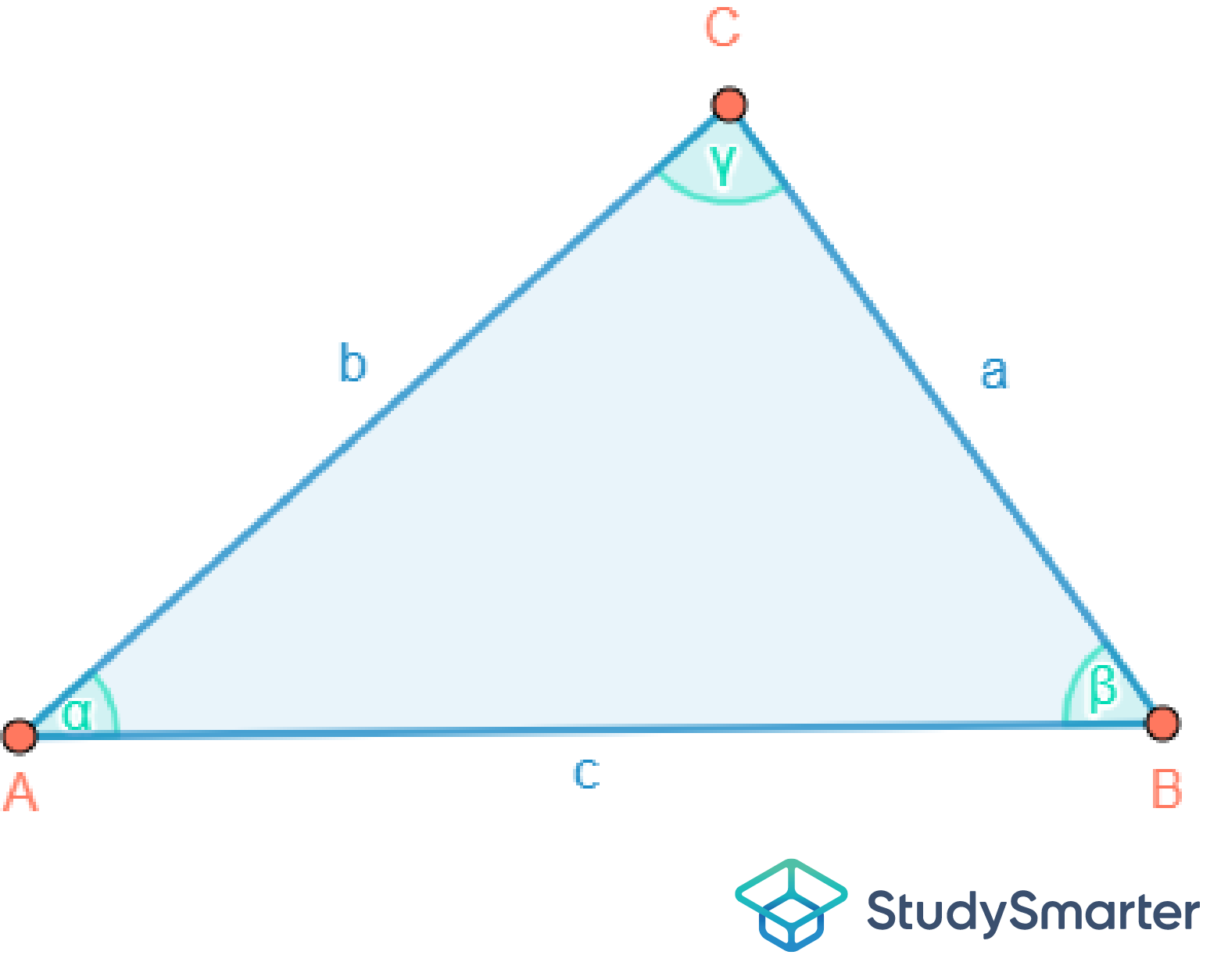
Abbildung 5: Spitzwinkliges Dreieck | 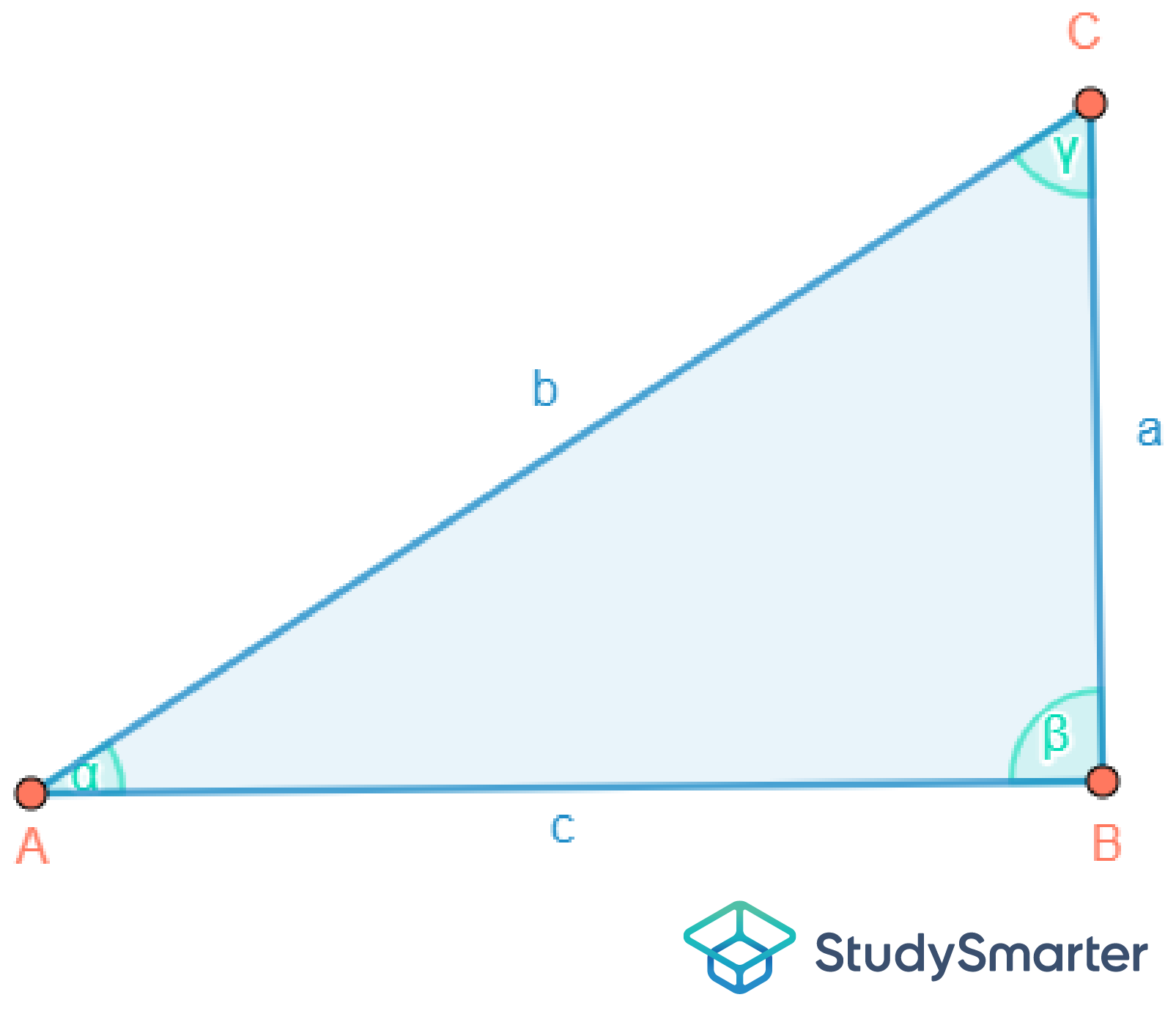
Abbildung 6: Rechtwinkliges Dreieck | 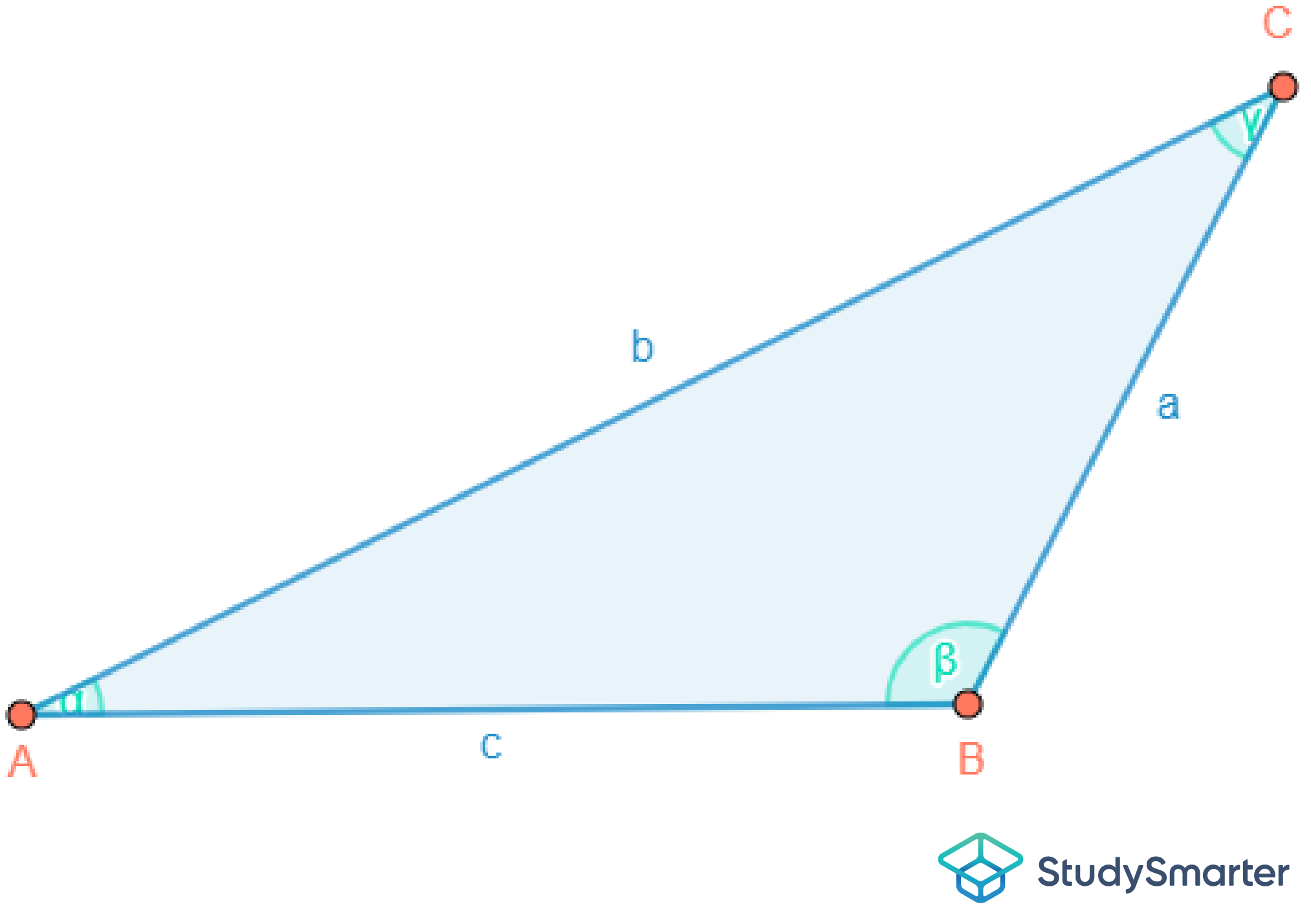
Abbildung 7: Stumpfwinkliges Dreieck |
Diese Dreiecke werden nach ihren größten Winkeln benannt. Mithilfe folgender Übersicht, kannst du schnell erkennen, um welche Art von Winkel es sich handelt.
Spitzwinkliges Dreieck
Rechtwinkliges Dreieck
Stumpfwinkliges Dreieck
Übrigens: Die Größe eines Winkels wird in Grad angegeben und kann mit einem Geodreieck bzw. Winkelmesser gemessen werden. Je größer der Winkel, umso größer die "Öffnung" des Winkels.
Da du nun sicherlich schon ganz neugierig darauf wartest, was ein gleichseitiges Dreieck besonders macht und wie man Kennzahlen wie Höhe, Fläche oder Umfang berechnet, lassen wir dich nicht länger damit warten.
Gleichseitiges Dreieck Eigenschaften und Größe
Hinter der spannenden Figur, dem gleichseitigen Dreieck, verbergen sich noch zahlreiche weitere interessante Eigenschaften, welche ich dir nun näher bringen werde.
Gleichseitiges Dreieck Seiten
Das gleichseitige Dreieck unterscheidet sich vom allgemeinen Dreieck darin, dass jede einzelne der drei Seiten immer gleich lang ist. Da wir bereits geklärt haben, dass jeder Kleinbuchstabe im Dreieck stellvertretend für einen bestimmten Wert steht, können wir also alle Seiten mit dem selben Buchstaben a versehen, wie in der folgenden Abbildung 10 dargestellt wird.
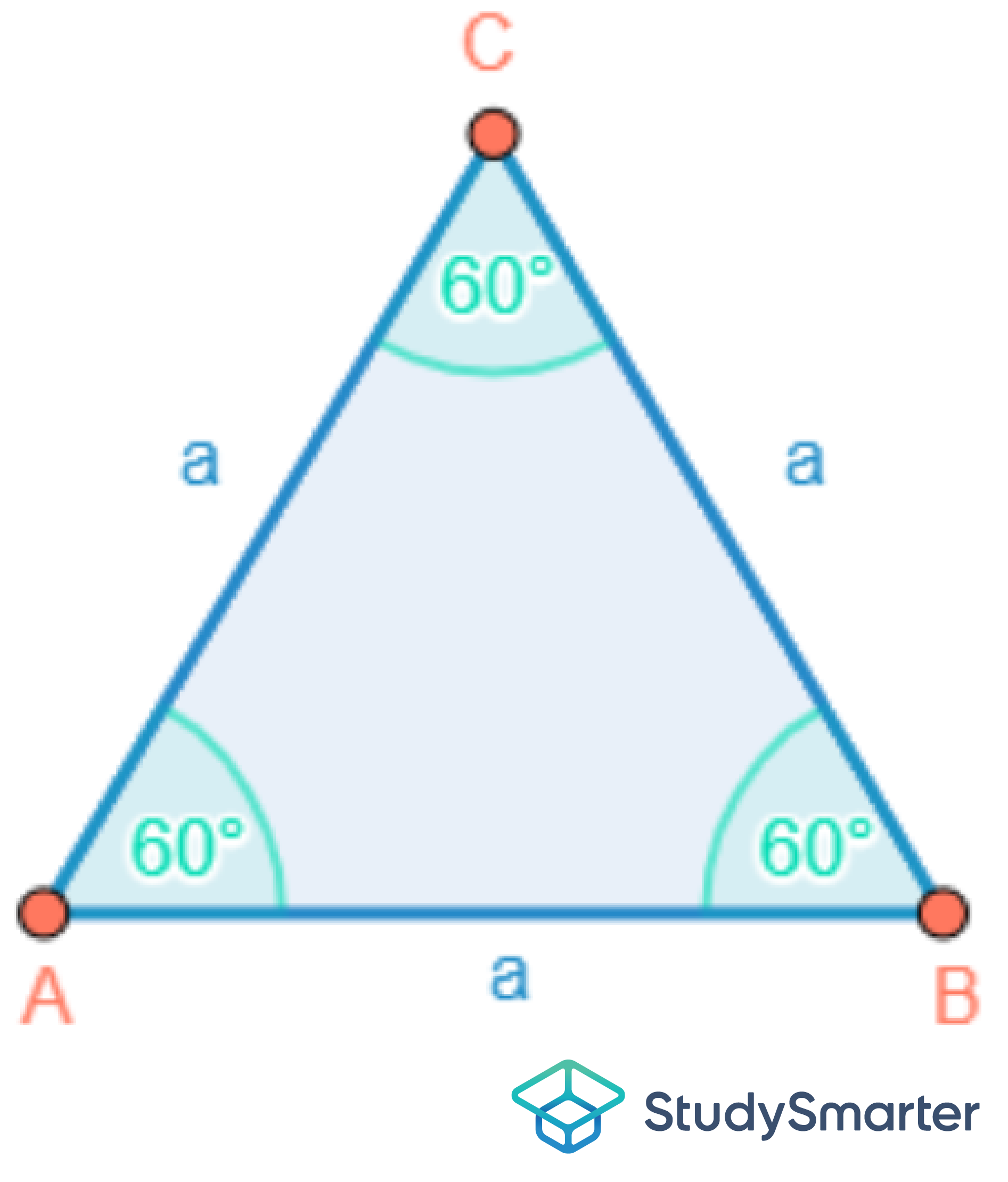
Abbildung 10: Gleichseitiges
DreieckHierbei wird immer der erste Buchstabe des Alphabets, also das kleine a verwendet.
Gleichseitiges Dreieck Winkel
Im gleichseitigen Dreieck sind immer alle Winkel gleich groß. Da jedes Dreieck, unabhängig von der Art des Dreiecks immer eine Winkelsumme von 180° hat, bedeutet dies, dass im gleichseitigen Dreieck jeder Winkel 60° groß ist. Das ergibt sich aus der Division von 180° mit. Damit erhalten wir 60° für jeden Winkel. Sieh dir dazu die korrekte Winkelbeschriftung in Abbildung 12 an.
Unter einer Winkelsumme versteht man übrigens die Summe aller drei Winkel.
Diese Abbildungen sollen dir helfen zu verstehen, inwiefern sich die Beschriftung des gleichseitigen Dreiecks von einem allgemeinen Dreieck unterscheidet.
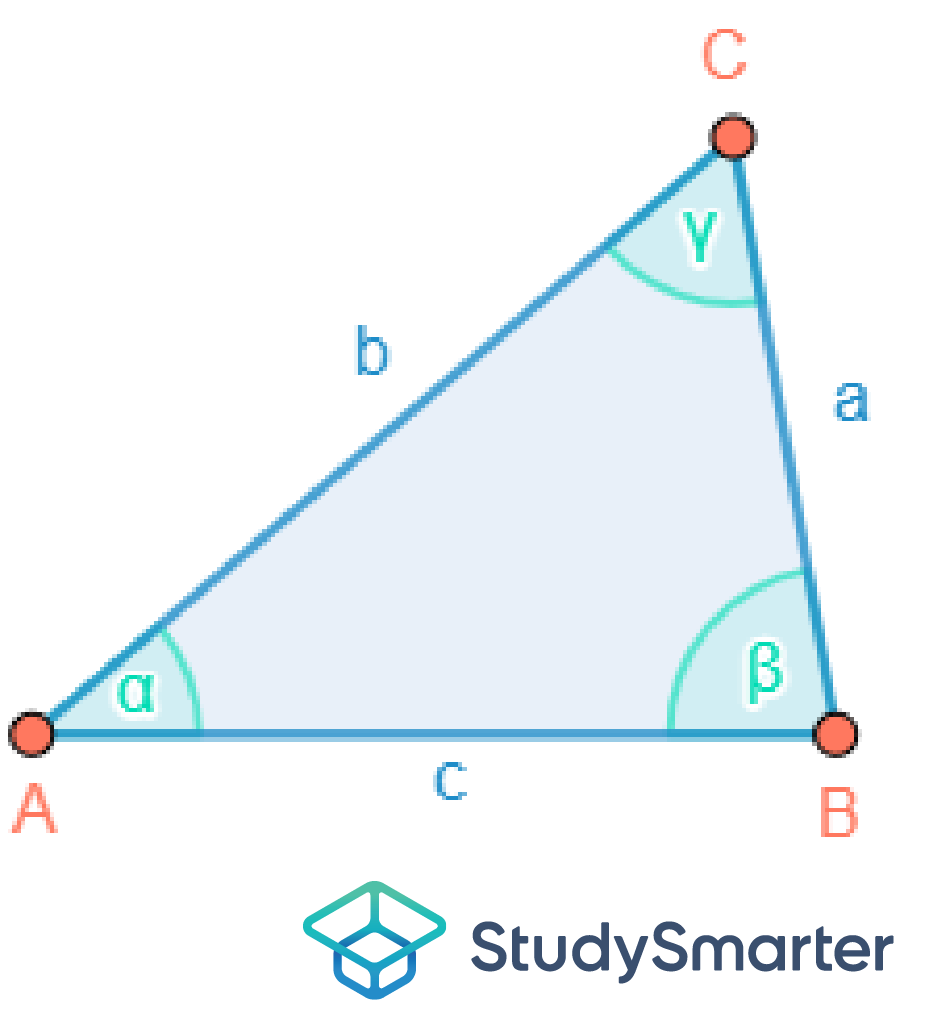
Abbildung 11: Allgemeines Dreieck
 Abbildung 12: Gleichseitiges Dreieck
Abbildung 12: Gleichseitiges Dreieck
Gleichseitiges Dreieck Höhe
Unter der Höhe versteht man in einem Dreieck eine Senkrechte auf die Grundlinie, welche zum gegenüberliegenden Eckpunkt verläuft.
Für das Dreieck gilt:



Die Höhe einer Seite wird mit dem Buchstaben "h" versehen, welcher um die Bezeichnung der Seite im Index ergänzt wird.
Du fragst dich bestimmt, warum wir überhaupt eine Höhe benötigen. Sehen wir uns dazu ein Beispiel an.
Aufgabe
Stell dir ganz einfach einen Sachverhalt aus dem alltäglichen Leben vor. Dein Freund behauptet, dass du es nicht schaffst, ein Kartenhaus mit Spielkarten zu bauen. Dabei müssen deine Karten genau eine Kartenlänge voneinander entfernt sein, wie bildlich in Abbildung 13 dargestellt wird.
 Abbildung 13: Kartenhaus aus Spielkarten
Abbildung 13: Kartenhaus aus Spielkarten
Nachdem du deinem Freund dein Talent als Kartenhausbauer unter Beweis stellen konntest, stellt er dich erneut unter die Probe. Er bietet dir 5 €, wenn du es schaffst die Höhe des Kartenhauses zu berechnen, wenn eine Karte8 cm hoch ist.
Du nimmst das Angebot voller Freude an, denn wie dir aufgefallen ist, besteht dein Kartenhaus nun aus zwei gleichseitigen Dreiecken und zufälligerweise kannst du dich noch an die Formel erinnern, welche man verwendet, um im gleichseitigen Dreieck die Höhe auszurechnen.
Lösung
Schauen wir uns die Berechnung der Höhe eines gleichseitigen Dreiecks in dem folgenden Beispiel an. Die zwei blauen Seiten a stellen dabei die Karten dar. Sie sind dabei im selben Abstand a (rot) zueinander aufgebaut.
a = 8 cm h = ? cm
 Abbildung 14: Gleichseitiges Dreieck
Abbildung 14: Gleichseitiges Dreieck
Sofort kannst du dich an die spannenden Geometrie Stunden erinnern und schreibst die Höhenformel im gleichseitigen Dreieck nieder, welche wie folgt lautet:

Als Nächstes setzt du in der Formel anstelle des Buchstabens "a" die Seitenlänge der Spielkarten ein und rechnest das Ergebnis für die Höhe mithilfe deines Taschenrechners aus.

Dein Freund ist sprachlos und nimmt direkt sein Lineal um die Höhe abzumessen und stellt fest, dass deine Berechnung einwandfrei war. Ohne ein Wort zu sagen gibt er dir seine versprochenen 5 €.
Gleichseitiges Dreieck Symmetrie
Unter dem Begriff Symmetrie versteht man, dass sich eine Figur an einem bestimmten Punkt oder einer Linie spiegelt. Diese Linie wird auch als Symmetrieachse bezeichnet.
In einem Dreieck können die Symmetrieachsen wie folgt eingezeichnet werden.
 Abbildung 15: Symmetrieachsen
Abbildung 15: Symmetrieachsen
Wie du nun feststellen konntest, entspricht die Höhe aller drei Seiten einer Symmetrieachse, also jener Linie, an welcher die Figur gespiegelt werden kann. Das gleichseitige Dreieck hat also immer drei Symmetrieachsen.
Gleichseitiges Dreieck Seitenhalbierende
Die Seitenhalbierende ist die Strecke vom Mittelpunkt einer Seite zur gegenüberliegenden Ecke. Der Schnittpunkt der Seitenhalbierenden ist zugleich der Mittelpunkt des Inkreises. Es gilt:

Zeichnen wir nun die Seitenhalbierenden in einem gleichseitigen Dreieck ein, so erhalten wir folgendes Bild.
 Abbildung 16: Seitenhalbierende
Abbildung 16: Seitenhalbierende
Die Seitenhalbierende werden mit dem Buchstaben "S" bezeichnet, gefolgt von der Beschriftung der Seiten im Index.
Gleichseitiges Dreieck Winkelhalbierende
Unter dem Begriff der Winkelhalbierenden versteht man einen Strahl, welcher in den Eckpunkten entspringt und den Winkel in zwei gleich große Teile teilt.
Für die Winkelhalbierenden im gleichseitigen Dreieck gilt:

Die Winkelhalbierenden werden mit dem Buchstaben "W", gefolgt von der Beschriftung der Winkel im Index, bezeichnet.
 Abbildung 17: Winkelhalbierende
Abbildung 17: Winkelhalbierende
Ich bin mir sicher du hast bemerkt, dass im gleichseitigen Dreieck die Linien der Seitenhalbierenden genau mit den Winkelhalbierenden übereinstimmen, welche wiederum genau die Höhen der einzelnen Seiten bzw. die Symmetrieachsen sind. Vergleiche hierfür die Abbildungen 15, 16 und 17.
Gleichseitiges Dreieck Inkreis
Der Inkreis ist der größtmögliche Kreis innerhalb der Figur, welcher alle Seiten der Figur berührt.
Die Formeln für den Inkreisradius r lauten:

Um den Inkreis zeichnen zu können, benötigt man den Radius des Innkreises. Danach geht es ganz einfach. Sieh dir dazu einfach die Abbildung 18 an.
 Abbildung 18: Inkreis
Abbildung 18: Inkreis
Der Mittelpunkt M stellt zugleich den Schwerpunkt des Dreiecks dar!
Gleichseitiges Dreieck Umkreis
Der Umkreis stellt einen Kreis dar, welcher die Figur umschließt und dabei alle Eckpunkte berührt.
Die Formel für den Umkreisradius r lautet:

Um den Umkreis einzeichnen zu können benötigt man den Radius des Umkreises.
 Abbildung 19: Umkreis
Abbildung 19: Umkreis
Um sowohl den Inkreis als auch den Umkreis im gleichseitigen Dreieck einzeichnen zu können, musst du zuerst den Mittelpunkt des Dreiecks bestimmen, welches jener Punkt ist, an welchem sich alle Winkelhalbierenden bzw. Seitenhalbierenden schneiden. Im Anschluss daran kannst du mit dem Zirkel genau an diesem Punkt einstechen und diesen so weit öffnen, bis die Öffnung genau dem zuvor ausgerechneten Radius entspricht.
Lass uns nun zum rechnerischen Teil dieser Beitrages übergehen, bei welchem wir mithilfe verschiedener Formeln die Fläche und den Umfang ausrechen werden.
Gleichseitiges Dreieck Fläche
Eine Fläche gibt an, wie groß etwas im zweidimensionalen Raum ist. Die Formel für die Berechnung der Fläche des gleichseitigen Dreiecks lautet.
Diese Definition soll in Abbildung 20 verdeutlicht werden.
 Abbildung 20: Fläche eines Dreiecks und eines Quadrats
Abbildung 20: Fläche eines Dreiecks und eines Quadrats
Die in dieser Abbildung blau markierte Größe, auch Fläche genannt, hilft dir, damit du mehrere Figuren auf ihre Größe vergleichen kannst. Du siehst, dass das hier dargestellte Quadrat größer als das Dreieck ist, es hat also eine größere Fläche als das Dreieck.
Die Fläche wird immer mit einem großen A gekennzeichnet.
Um bei Dreiecken allgemein die Fläche ausrechnen zu können, benötigt man meistens die senkrechte Linie auf die Grundlinie, auch Höhe genannt. Wenn wir nun die Grundlinie bzw. die Seite a mit der Höhe multiplizieren, also genau wie uns die erste Formel vorschreibt, erhalten wir folgende Figur:
 Abbildung 21: Fläche im Dreieck
Abbildung 21: Fläche im Dreieck
Wie man in Abbildung 21 erkennen kann, erhält man indem man a ⋅ h rechnet ein Rechteck, welches die Figur umschließt. Bei genauerem Hinsehen merkt man, dass das Rechteck genau doppelt so groß ist wie das Dreieck. Dies bestätigt die Aussage, dass die Formel für die Fläche jeder Dreiecksart  .
.
Für das gleichseitige Dreieck gibt es folgende Alternativformel für die Flächenberechnung, sollte die Höhe nicht gegeben sein:

Am Ende dieses Beitrages findest du Übungsaufgaben, bei welchen wir unser Wissen zu Umfang und Fläche vertiefen werden, also bleib dran.
Gleichseitiges Dreieck Umfang
Unter dem Umfang versteht man die Summe aller Seitenlängen, welche die Figur begrenzen.
Somit gilt für das gleichseitige Dreieck:

Den Umfang benötigst du im täglichen Leben öfter als du vielleicht denkst. Stell dir vor du musst deine Wiese einzäunen und möchtest wissen, wie viel Meter Zaun du insgesamt benötigst. Genau hier kommt der Umfang ins Spiel.
Der Umfang wird immer mit einem großen U gekennzeichnet.
Möchtest du also nun die Seite a bei gegebenen Umfang ausrechnen, müssen wir lediglich das " a " in der Umfangsformel freistellen.

Bevor wir zu den Übungsbeispielen übergehen, müssen wir uns noch unbedingt kurz einen höchstwichtigen Satz ansehen, welcher es dir ermöglicht, die Höhe im gleichseitigen Dreieck zu berechnen.
Gleichseitiges Dreieck Übungsaufgaben
Aufgabe 1
Welches der folgenden Dreiecke fällt unter die Kategorie "gleichseitiges Dreieck"?
![]()
![]()
 Abbildung 23: Dreiecke im Vergleich
Abbildung 23: Dreiecke im Vergleich
![]()
![]()
Die Lösung findest du unterhalb dieses Hinweises. Achtung: Sie ist rückwärts geschrieben.
Lösung
"githcir tsi kceierD etiewz saD"
Aufgabe 2
Folgende Seiten eines gleichseitigen Dreiecks sind gegeben:
a = 7 cm
h = 5 cm
Berechne den Umfang und die Fläche!
 Abbildung 24: Gleichseitiges Dreieck
Abbildung 24: Gleichseitiges Dreieck
Lösung
Berechnung des Umfangs
Um den Umfang des Dreiecks auszurechnen, bedienen wir uns der Formel U = 3 ⋅ a. Wir zählen also alle Seitenlinien, welche die Figur begrenzen, zusammen.
Auf unser Beispiel bezogen sieht dies wie folgt aus:

Somit beträgt der Umfang des Dreiecks 21 cm.
Berechnung der Fläche
Da in unserem Beispiel die Höhe in der Angabe bereits einen Wert aufweist, können wir die Formel  verwenden.
verwenden.
Auf unser Beispiel bezogen sieht dies wie folgt aus:

Somit beträgt die Fläche des Dreiecks 17,5 cm².
Beachte, dass die Einheit der Fläche immer mit hoch " 2 " versehen wird, da wir uns nun im Zweidimensionalen befinden.
Aufgabe
Folgende Seiten eines gleichseitigen Dreiecks sind gegeben:
a = 10cm
Berechne den Umfang und die Fläche!
 Abbildung 25: Skizze
Abbildung 25: Skizze
Lösung
Berechnung des Umfangs
Für die Berechnung des Umfangs verwenden wir erneut die Formel U = 3 ⋅ a.
Setzen wir die Werte unseres Beispiels in die Formel ein, erhalten wir folgendes:

Der Umfang des Dreiecks beträgt also insgesamt 30 cm.
Berechnung der Fläche
Da wir in diesem Beispiel die Höhe nicht gegeben haben, bedienen wir uns der Alternativformel für die Berechnung der Fläche des gleichseitigen Dreiecks, welche wie folgt lautet:

Setzen wir nun unseren Wert für a in diese Formel ein, erhalten wir folgendes Ergebnis:


Die Fläche des gleichseitigen Dreiecks mit der Seite a von 10 cm beträgt 43,30 cm².
Gleichseitiges Dreieck - Das Wichtigste



































 .
.







 verwenden.
verwenden.






 .
.






