Stell Dir vor, Du machst mit einem Deiner Freunde ein Wettrennen auf dem Sportplatz Eurer Schule. Die Sportbahn ist rund, mit einer kreisförmigen Grasfläche in der Mitte.
Dein Freund läuft auf der inneren Linie, während Du ganz außen läufst. Wie viel mehr Strecke musst Du laufen? Diese Antwort kann man mit dem Umfang eines Kreisrings berechnen. Und genau das wirst Du in diesem Artikel lernen.
Umfang Kreisring – Erklärung
Kreisring – Definition
Ein Kreisring ist die Fläche, welche zwischen zwei unterschiedlich großen Kreisen mit demselben Mittelpunkt liegt. Aufgrund dessen hat ein Kreisring zwei verschiedene Radien: \(r_k\), der Radius des kleinen Innenkreises und \(r_g\), der Radius des größeren Außenkreises. Beide dieser Radien – und damit beide Kreise – haben den gleichen Mittelpunkt M.
Abbildung 1: Kreisring
Umfang Kreisring – Formel
Stell Dir vor, es wird ein Verkehrskreisel mit einer mit Blumen bepflanzten Insel in der Mitte gebaut. Der Asphalt ist schon fertig und es fehlt nur noch ein Bordstein an beiden Seiten der Fahrbahn. Wie viele Steine müssen gekauft werden, dass es für einen Bordstein an beiden Seiten der Fahrbahn reicht? Je nach Größe des Kreisels ändert sich auch die Menge an Steinen, die benötigt werden. Der Umfang gibt dabei genau an, wie lang die Strecke an beiden Seiten der Fahrbahn ist.
Der Umfang eines Kreisrings ist die Länge der Strecke, die den Kreisring außen begrenzt, addiert mit der Länge der Strecke, die den Kreisring innen begrenzt.
Der Umfang wird mit dem Großbuchstaben U abgekürzt und wir mit \begin{align}U_{Ring} &= U_{g}+U_{k}\\&=2\pi\cdot r_{g}+2\pi\cdot r_{k}\\&=2\pi\cdot(r_{g}+r_{k})\end{align}
Umfang eines Kreisrings berechnen
In diesem Kapitel kannst Du Deine oben gelernten Erkenntnisse testen und tatsächlich den Umfang eines Kreisrings berechnen. Dazu findest Du hier für jede Möglichkeit eine Übungsaufgabe.
Umfang eines Kreisrings mit dem Radius berechnen
In diesem Beispiel kannst Du den Umfang eines Kreisrings mit dem Radius und der dazu passenden Formel berechnen:
Aufgabe 1
Berechne den Umfang U eines Kreisrings mit den Radien \(r_g = 5\, cm\) und \(r_k=2\, cm\).
Lösung:
Schreibe als Erstes die Formel auf. In diesen Fall ist der Radius gegeben, daher wählt man:
\[U=2\pi\cdot(r_{g}+r_{k})\]
Setze als Nächstes die Werte für r, in diesem Fall 5 cm und 2 cm, in die Formel ein:
\[U=2\pi\cdot(5\, cm+2\, cm)\]
Zuletzt berechnest Du das Ergebnis mit dem Taschenrechner:
\[U=2\pi\cdot7\, cm\approx 43{,}98\, cm\]
Auf den meisten Taschenrechnern gibt es eine Taste, um Pi einzusetzen. Hast Du die nicht, kannst Du bei der Berechnung des Flächeninhalts auch ausnahmsweise einfach den gerundeten Wert von 3,41 verwenden.
Der Kreisring hat also einen Umfang von rund \( 43{,}98\, cm\).
Zusammengefasst besteht diese Berechnungsart also aus drei Schritten:
- Formel aufschreiben,
- Werte einsetzen,
- Ergebnis ausrechnen.
Umfang eines Kreisrings mit dem Durchmesser berechnen
In diesem Beispiel wird der Umfang eines Kreisrings mit dem Durchmesser und der dazu passenden Formel berechnet:
Aufgabe 2
Berechne den Umfang U eines Kreisrings mit den Durchmessern \(d_g=4\, cm\) und \(d_k=1\, cm\).
Lösung
Als Erstes wird die passende Formel ausgesucht. Da der Durchmesser gegeben ist, wählt man folgende Formel:
\[U=2\pi\cdot\frac{d_g}{2}+2\pi\cdot\frac{d_k}{2}\]
Im nächsten Schritt werden die gegebenen Werte, also \(d_g=4\, cm\) und\(d_k=1\, cm\), in die Formel eingesetzt:
\[U=2\pi\cdot\frac{4\, cm}{2}+2\pi\cdot\frac{1\, cm}{2}\]
Zum Schluss kannst Du jetzt das Ergebnis wieder mit dem Taschenrechner ausrechnen:
\[U=2\pi\cdot 2\, cm+2\pi \cdot 0{,}5\, cm\approx 15{,}71\, cm\]
Dadurch, dass π eine unendliche Zahl ist, hat auch der Flächeninhalt eines Kreisrings meistens sehr viele Nachkommastellen. Diese musst du aber nicht alle aufschreiben. Du kannst einfach auf zwei Nachkommastellen runden.
Der Umfang U beträgt gerundet \(15{,}71\, cm\).
Zusammengefasst besteht auch diese Berechnungsart, genau wie bei der Berechnung mit dem Radius, aus drei Schritten:
- Formel aufschreiben,
- Werte einsetzen,
- Ergebnis ausrechnen.
Umfang eines Kreisrings mit dem Flächeninhalt berechnen
Was machst Du, wenn Du weder die Radien r noch die Durchmesser d eines Kreisrings gegeben hast? Kann der Umfang dann auch berechnet werden? Die Antwort ist ja, wenn Du die Flächeninhalte des inneren und des äußeren Kreises gegeben hast:
Aufgabe 3
Gegeben sind die Flächeninhalt \(A_g=30\, cm^2\) und \(A_k = 20\, cm^2\) eines Kreisrings. Du sollst jetzt daraus den Umfang U berechnen.
Lösung
Zuerst wird die Formel für den Flächeninhalt eines Kreises aufgeschrieben:
\[A=\pi \cdot r^2\]
Wenn du dir nicht mehr sicher bist, was genau der Flächeninhalt eines Kreises ist und mehr Infos dazu willst, lese dir doch unseren Artikel zum Thema Flächeninhalt eines Kreises durch.
Als Nächstes stelle die Formel um, sodass der Radius r ausgerechnet werden kann:
\begin{align} A&=\pi \cdot r^2 \quad&&|:\pi\\r^2&=\frac{A}{\pi}&&|\sqrt{ }\\r&=\sqrt{\frac{A}{\pi}}\end{align}
Jetzt kannst Du die Formel für die Berechnung des Umfangs eines Kreisrings mit dem Radius aufschreiben.
\[U=2\pi\cdot r_g + 2\pi\cdot r_k\]
Da die Formel des Flächeninhalts oben umgestellt wurde, setze nun die umgestellte Formel in die Formel des Umfangs ein:
\[U=2\pi\cdot\sqrt{\frac{A_g}{\pi}}+2\pi\cdot\sqrt{\frac{A_k}{\pi}}\]
Als Letztes kannst Du die gegebenen Werte von \(A_g=30\,cm^2\) und \(A_k=20\, cm^2\) für die Flächeninhalte A einsetzen und das Ergebnis ausrechnen:
\[U=2\pi\cdot\sqrt{\frac{30\,cm^2}{\pi}}+2\pi\cdot\sqrt{\frac{20\,cm^2}{\pi}}=35{,}27\,cm\]
Der Umfang des Kreisrings beträgt ungefähr \(35{,}27\).
Zusammengefasst besteht diese Berechnungsart aus sechs Schritten:
- Formel für den Flächeninhalt aufschreiben,
- Formel nach r umstellen,
- Formel für Umfang mit r aufschreiben,
- r aus der umgestellten Formel in r der Formel des Umfangs einsetzen,
- Werte einsetzen,
- Ergebnis ausrechnen.
Innerer Ring und äußerer Ring
Flächeninhalt eines Kreisrings
Es kann nicht nur mithilfe des Flächeninhalts der Umfang eines Kreisrings berechnet werden, es kann auch der Flächeninhalt des Kreisrings selbst berechnet werden.
Wie du eben schon gemerkt hast, gibt es auch hier zwei verschiedene Flächeninhalte:
- Der Flächeninhalt des inneren, kleinen Kreises
- Der Flächeninhalt der äußeren, großen Kreises
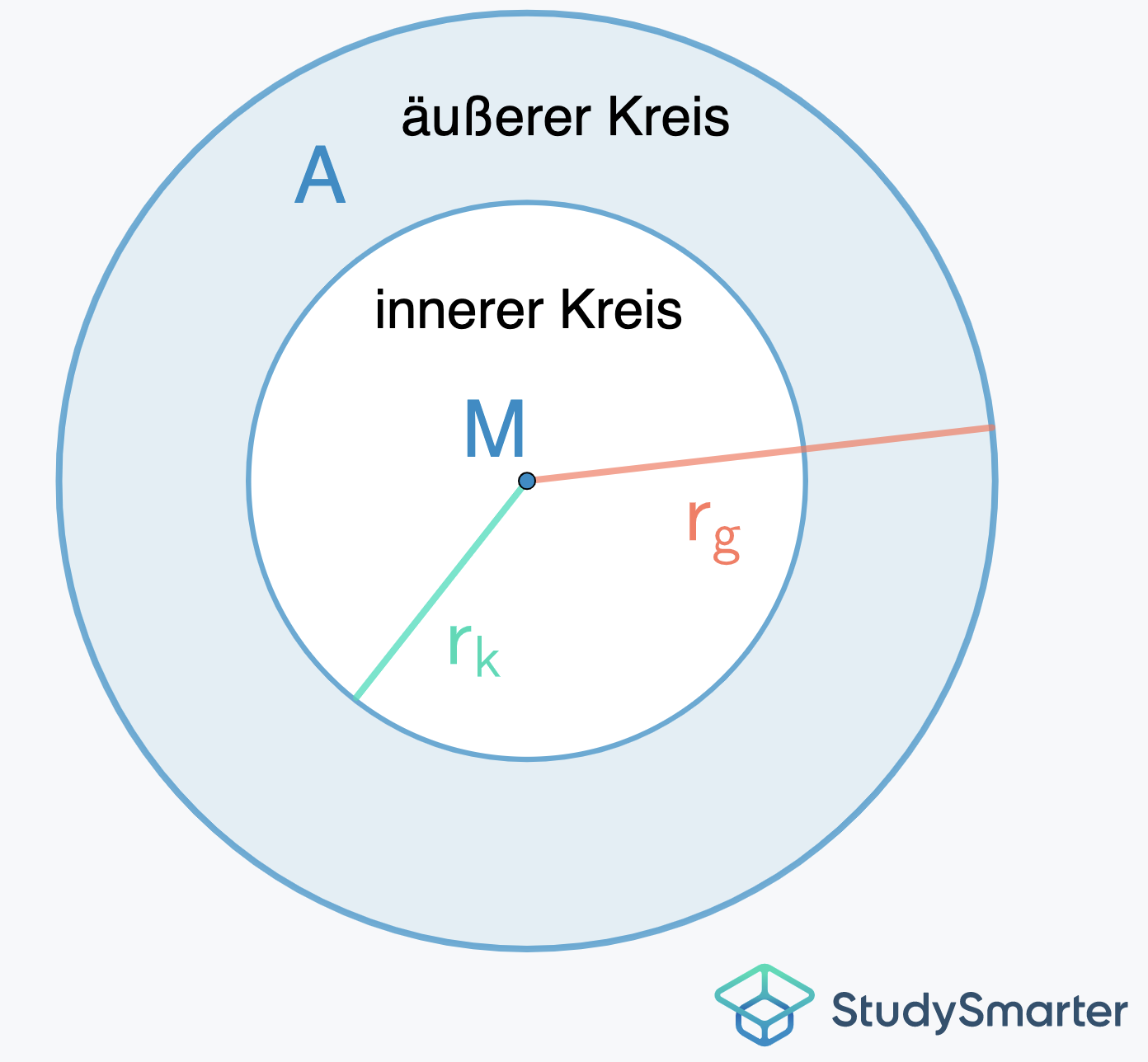
Abbildung 3: Flächeninhalt Kreisring
Um den Flächeninhalt des Kreisrings zu berechnen, musst du einfach den Flächeninhalt des großen Kreises berechnen und dann den Flächeninhalt des kleinen Kreises abziehen. Und schon hast du nur noch den Unterschied zwischen dem großen und dem kleinen Kreis, also den Kreisring.
Für den Flächeninhalt A eines Kreisrings gilt:
\[A=\pi\cdot r_g^2-\pi\cdot r_k^2\]
oder
\[A=\pi\cdot \left(\frac{d_g}{2}\right)^2-\pi\cdot \left(\frac{d_k}{2}\right)^2\]
Umfang eines Kreisrings – Übungsaufgaben
In den folgenden Übungsaufgaben kannst Du Dein Wissen testen!
Aufgabe 4
Wenn Du zurück an den Bordstein denkst, der auf beiden Seiten einer Verkehrskreisel-Fahrtbahn gebaut werden soll. Der Kreisel hat einen Innendurchmesser von \(d_k=68\, m\) und einen Außenradius von \(d_g=40\, m\).
Wie viele Steine werden gebraucht, um den Bordstein zu bauen, wenn ein Stein 10 cm lang ist?
Lösung
Als Erstes kannst du dir eine Zeichnung der Situation anlegen. Die 40 m sind der Außenradius, während die 68 m der Durchmesser des inneren Kreises sind. Du sollst die Länge der Bordsteine, also den Umfang des Kreisrings, berechnen.
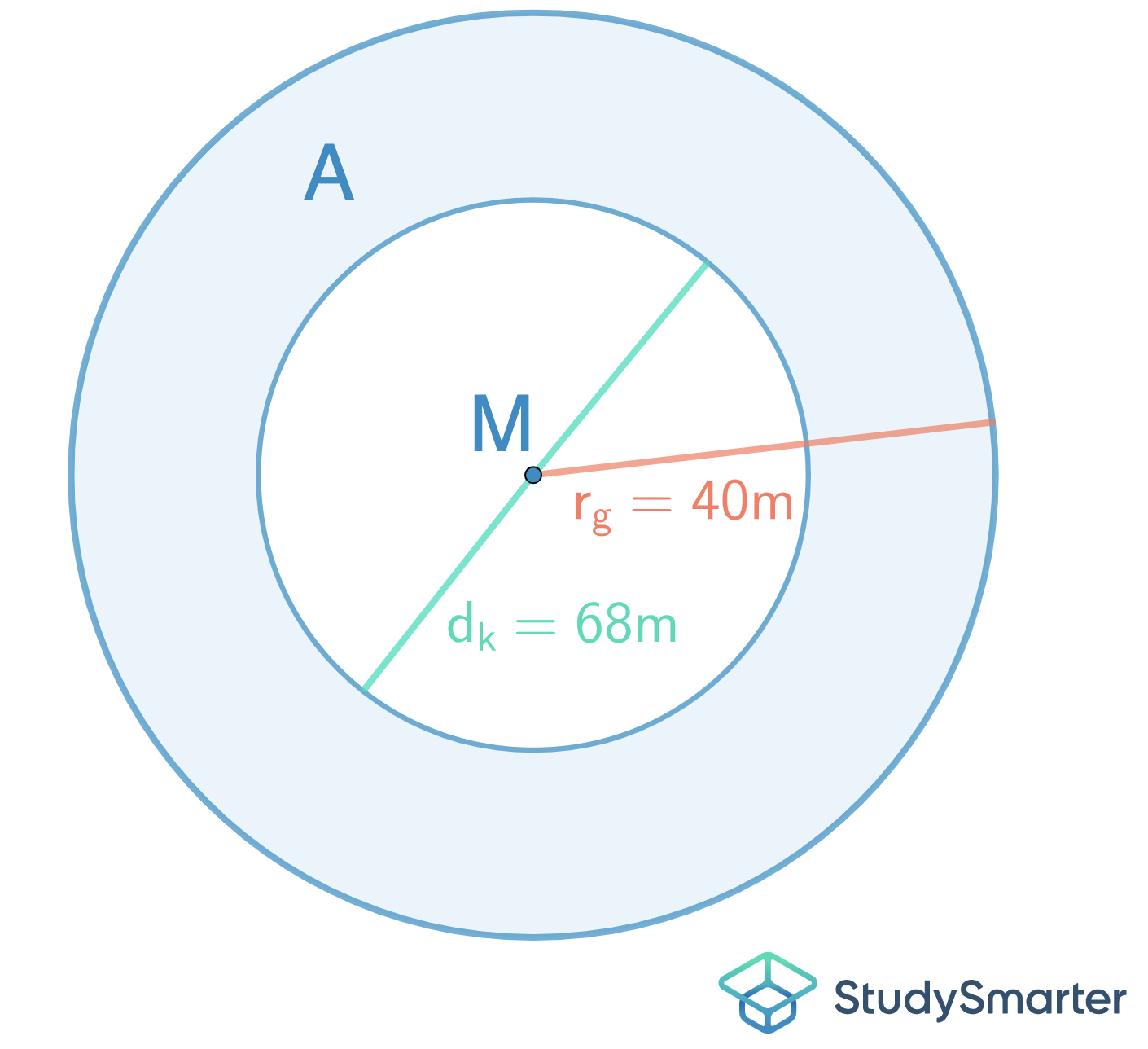
Abbildung 4: Verkehrskreisel Zeichnung
Dann musst Du entweder die 40 m Radius in einen Durchmesser oder die 68 m Durchmesser in einen Radius umrechnen. In diesem Fall wird alles in einen Radius umgewandelt.
Du schreibst Dir also das Verhältnis zwischen dem Durchmesser und dem Radius auf, setzt die 68 m ein und berechnest das Ergebnis.
\begin{align}r&=\frac{d}{2}\\&=\frac{68\, m}{2}\\&=34\, m\end{align}
Als Nächstes kannst Du die Formel zur Berechnung des Umfangs eines Kreisrings mit dem Radius aufschreiben. Dann kannst Du die Werte einsetzen und das Ergebnis berechnen.
\begin{align} U&=2\pi\cdot r_g+2\pi\cdot r_k\\&=2\pi \cdot 40\, m+2\pi\cdot 34\, m\\&\approx 465\, m\end{align}
Jetzt weißt Du, wie lang die Strecke ist, die mit Steinen ausgelegt werden soll. Jetzt musst Du nur noch herausfinden, wie viele Steine Du legen musst, um auf diese 465 m zu kommen. Um das zu berechnen, kannst Du genau diesen Sachverhalt einmal mathematisch aufschreiben und dann auflösen.
\begin{align} 0{,}1\cdot x&= 465\, m\quad | :0{,}1\, m \\ x&= 4650\end{align}
Es werden also genau 4650 Steine gebraucht, um den Bordstein zu bauen.
Aufgabe 5
Erinnerst du dich noch an die Einleitung? Du und ein Freund macht ein Wettrennen, aber er läuft auf der Innenbahn, während du auf der Außenbahn eines runden Sportfeldes läufst. Das Sportfeld ist auf einer Fläche von 12000 m². Die Grasfläche in der Mitte ist 4800 m² groß.
Wie viel mehr Weg als er musst du zurücklegen?
Lösung
Als Erstes musst du erkennen, welche Werte gesucht und welche Werte gegeben sind.
Gesucht ist der Wegunterschied zwischen dem Umfang des inneren Kreises und dem Umfang des äußeren Kreises. Gegeben ist der Flächeninhalt A des größeren Kreises und der Flächeninhalt A des kleinen Kreises.
Um das Ergebnis berechnen zu können, musst du also diesmal nicht, wie bisher, die Umfänge der beiden Kreise addieren, sondern du musst sie subtrahieren, um auf den Wegunterschied zu kommen.
\begin{align}\Delta U&=U_g-U_k\\&=2\pi \cdot r-g -2\pi \cdot r_k\end{align}
Da Du aber nicht den Radius r gegeben hast, sondern den Flächeninhalt A, musst Du erst die Formel für den Flächeninhalt eines Kreises aufschreiben und diese nach r umstellen.
\begin{align} A&=\pi \cdot r^2 \quad |:\pi\\r^2&=\frac{A}{\pi}\\r&=\sqrt{\frac{A}{\pi}}\end{align}
Diese Formel musst Du jetzt in die Formel einsetzen, die Du als Erstes aufgestellt hast. Dann kannst Du die Werte einsetzen und das Ergebnis berechnen.
\begin{align} \Delta U &= 2\pi \cdot \sqrt{\frac{A_g}{\pi}}-2\pi \cdot \sqrt{\frac{A_k}{\pi}}\\&=2\pi \cdot \sqrt{\frac{12000\,m^2}{\pi}}-2\pi \cdot \sqrt{\frac{4800\,m^2}{\pi}}\\&\approx 143\, m\end{align}
Du musst also ungefähr 143 m mehr laufen als dein Freund.
Umfang eines Kreisrings – Das Wichtigste auf einen Blick
- Der Umfang U eines Kreisrings ist abhängig von seinem Außenradius \(r_g\) und seinem Innenradius \(r_k\) bzw. seinem Außendurchmesser \(d_g\) und seinem Innendurchmesser \(d_k\)
- Für den Umfang U eines Kreisrings mit dem Radius r gilt: \(U=2\pi \cdot r_g+2\pi\cdot r_k\)
- Für den Umfang U eines Kreisrings mit dem Durchmesser d gilt: \(U=2\pi \cdot \frac{d_g}{2}+2\pi \cdot \frac{d_k}{2}\)
- Es müssen drei Schritte befolgt werden beim Rechnen mit diesen Formeln:
- Formel aufschreiben,
- Werte einsetzten,
- Ergebnis ausrechnen.
- Für einen Kreisring mit dem Umfang U und den Flächeninhalten \(A_g\) und \(A_k\) gilt: \(U=2\pi\cdot \sqrt{\frac{A_g}{\pi}}+2\pi\cdot \sqrt{\frac{A_k}{\pi}}\)
- Für den Flächeninhalt eines Kreisrings gilt: \(A=\pi\cdot r_g^2-\pi \cdot r_k^2\)
Erklärungen 
Magazine 
